정사영 (Orthogonal Projection)
$ \mathbb{R}^3 $ 의 벡터 $ \mathbf{x} = \overrightarrow{OP} $ 와 $ \mathbf{y} = \overrightarrow{OQ} \leq \mathbf{0} $ 가 있을 때, 점 $ P $ 에서 직선 $ OQ $ 에 내린 수선읠 발을 $ R $ 이라 하면 벡터 $ \mathbf{x_1} = \overrightarrow{OR} $ 을 $ \mathbf{y} $ 위로의 $ \mathbf{x} $ 의 정사영이라 한다.
정사영은 다음과 같이 나타낸다.
$$ \mathbf{x_1} = \operatorname{proj}_\mathbf{y} \mathbf{x} $$
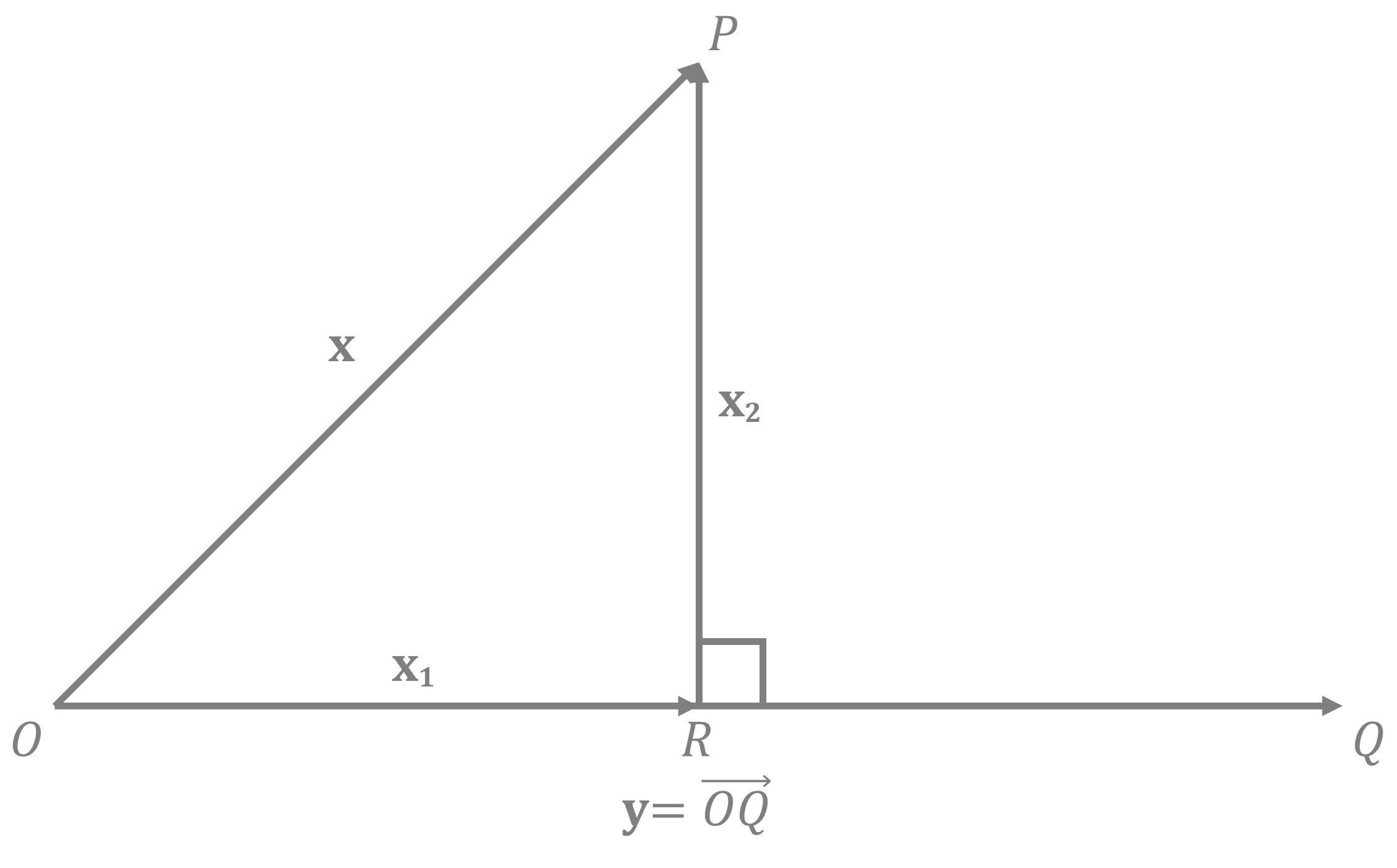
이때 $ \mathbf{x_2} = \overrightarrow{RP} $ 를 $ \mathbf{y} $ 에 수직인 $ \mathbf{x} $ 의 벡터성분(vector component)이라 한다. 따라서 $ \mathbf{x} = \mathbf{x_1} + \mathbf{x_2} $ 이다.
추가로 다음 성질이 성립한다. $ \mathbf{u} = \dfrac{\mathbf{y}}{\| \mathbf{y} \|} $ 일 때 $ \operatorname{proj}_{\mathbf{y}}\mathbf{x} = (\mathbf{x} \cdot \mathbf{u}) \mathbf{u} $ 이고, $ \| \operatorname{proj}_{\mathbf{y}}\mathbf{x} \| = | \mathbf{x} \cdot \mathbf{u} | $ 이다.
거리 공식
- 점과 직선 사이 거리
$ \mathbb{R}^3 $ 에서 한 점 $ P $ 와 직선 $ l $ 의 거리 $ L $ 은 직선 $ l $ 위의 서로 다른 점 $ Q $ 와 $ R $ 에 대하여 다음과 같다.
$$ L = \dfrac{\| \overrightarrow{QR} \times \overrightarrow{QP} \|}{\| \overrightarrow{QR} \|} $$
- 점과 평면 사이 거리
$ \mathbb{R}^3 $ 에서 한 점 $ P_0 (x_0, y_0, z_0) $ 와 평면 $ Ax+By+Cz = D $ 의 거리 $ L $ 은 다음과 같다.
$$ L = \dfrac{| A x_0 + B y_0 + C z_0 - D |}{\sqrt{A^2 + B^2 + C^2}} $$
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] 벡터공간(vector space)과 부분공간(subspace) (0) | 2024.10.18 |
|---|---|
| [Linear Algebra] 다차원 벡터(multidimensional vector) (0) | 2024.10.18 |
| [Linear Algebra] 공간벡터의 내적(inner product)과 외적(cross product) (0) | 2024.10.17 |
| [Linear Algebra] 벡터(vector)의 정의와 연산 및 성질 그리고 단위벡터(unit vector) (0) | 2024.10.17 |
| [Linear Algebra] 크라메르 공식(Cramer's rule) (0) | 2024.10.12 |