정규직교집합
내적공간의 원소 $ \mathbf{x} $ 와 $\mathbf{y} $ 에 대하여 $ \left< \mathbf{x}, \mathbf{y} \right> = 0 $ 일 때 두 벡터가 직교한다고 정의하였다. 만약 $ V $ 가 내적공간일 때 $ \mathbf{x_1}, \mathbf{x_2}, \cdots, \mathbf{x_n} \in V $ 에 대하여 $ S = \{ \mathbf{x_1}, \mathbf{x_2}, \cdots, \mathbf{x_n} \} $ 을 가정하자. 이때 $ S $ 의 서로 다른 두 벡터가 모두 직교한다면 $ S $ 를 직교집합(orthogonal set)이라 한다. 또한 직교집합 $ S $ 의 벡터가 모두 단위벡터이면 $ S $ 를 정규직교집합이라 한다.
즉 다음이 정의된다.
$ S \text{ } \text{ is orthogonal set} \quad \Longleftrightarrow \quad \left< \mathbf{x_i} , \mathbf{x_j} \right> = \begin{cases} 0, & (i \neq j) \end{cases} $
$ S \text{ } \text{ is orthonormal set} \quad \Longleftrightarrow \quad \left< \mathbf{x_i} , \mathbf{x_j} \right> = \begin{cases} 0 , & (i \neq j) \\ 1 , & (i = j) \end{cases} $
만약 $ S $ 가 내적공간의 표준기저라면 $ S $ 는 정규직교집합이다.
정규직교기저 (Orthonormal Basis)
$ V $ 가 내적공간일 때 $ V $ 의 원소이면서 영벡터가 아닌 벡터들의 집합 $ S = \{ \mathbf{x_1}, \mathbf{x_2}, \cdots, \mathbf{x_n} \} $ 가 직교집합이면 $ S$ 는 일차독립이다.
나아가 $ S $ 가 직교집합이면 $ S $ 를 직교기저(orthogonal basis)라 하고, 정규직교집합이면 정규직교기저라 한다. 따라서 표준기저는 정규직교기저이다.
내적공간에서 기저를 정규직교기저로 선택하면 편리한 점이 많은데, 예를 들어 $ S = \{ \mathbf{x_1}, \mathbf{x_2}, \cdots, \mathbf{x_n} \} $ 이 $ V $ 의 정교직교기저라면 $ \mathbf{v} \in V $ 는 다음과 같이 유일하게 나타낼 수 있다.
$$ \mathbf{v} = k_1 \mathbf{x_1} + k_2 \mathbf{x_2} + \cdots + k_n \mathbf{x_n} \quad (k_1, k_2, \cdots, k_n \in \mathbb{R} ) $$
이때 $ \left< \mathbf{x_i}, \mathbf{x_j} \right> =0 $ $(i \neq j) $ 임을 이용하면 $ k_1, k_2, \cdots, k_n $ 을 쉽게 구할 수 있다. 즉 다음과 같이 나타낼 수 있다.
$$ \mathbf{v} = \left< \mathbf{v}, \mathbf{x_1} \right> \mathbf{x_1} + \left< \mathbf{v}, \mathbf{x_2} \right> \mathbf{x_2} + \cdots + \left< \mathbf{v}, \mathbf{x_n} \right> \mathbf{x_n} $$
$ S = \{ \mathbf{x_1}, \mathbf{x_2}, \cdots, \mathbf{x_n} \} $ 는 $ V $ 의 기저이므로 $ V $ 의 벡터 $ \mathbf{v} $ 는 다음과 같이 나타낼 수 있다.
$ \mathbf{v} = k_1 \mathbf{x_1} + k_2 \mathbf{x_2} + \cdots + k_n \mathbf{x_n} \quad (k_1, k_2, \cdots, k_n \in \mathbb{R} ) $
이때 $ k_ i = \left< \mathbf{v}, \mathbf{x_i} \right> $ $ (i = 1, 2, \cdots, n) $ 임을 보이면 된다.
$ \left< \mathbf{v}, \mathbf{x_i} \right> = \left< k_1 \mathbf{x_1} + k_2 \mathbf{x_2} + \cdots + k_n \mathbf{x_n} , \mathbf{x_i} \right> $
$ = k_1 \left< \mathbf{x_1}, \mathbf{x_i} \right> + k_2 \left< \mathbf{x_2}, \mathbf{x_i} \right> + \cdots + k_i \left< \mathbf{x_i}, \mathbf{x_i} \right> + \cdots + k_n \left< \mathbf{x_n}, \mathbf{x_i} \right> $
이때 $ S $ 가 정규직교기저이므로 $ \left< \mathbf{x_i} , \mathbf{x_j} \right> = \begin{cases} 0 , & (i \neq j) \\ 1 , & (i = j) \end{cases} $ 이고, 따라서 $ \left< \mathbf{v} , \mathbf{x_i} \right> = k_i $ 이다.
정사영 벡터 (Orthogonal Projection Vector)
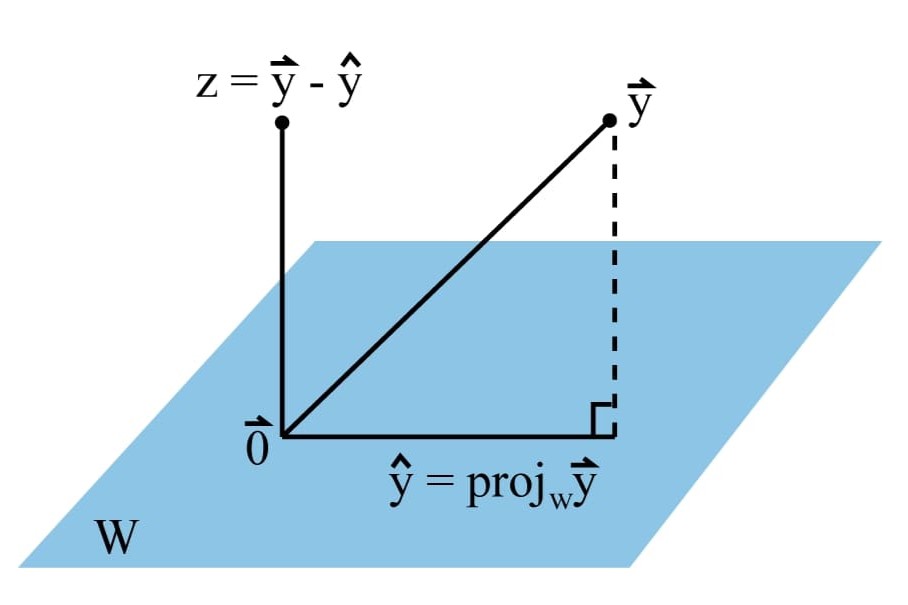
$ n $ 차원 내적공간 $ V $ 을 가정할 때 이 내적공간의 정규직교집합이 $ S = \{\mathbf{x_1} , \mathbf{x_2}, \cdots, \mathbf{x_m} \} $ 이고 $ W = \left< S \right> $ 라 할 때, $ V $ 의 벡터 $ \mathbf{y} $ 에 대하여 다음과 같다 하자.
$ \mathbf{y_1} = \left< \mathbf{y} , \mathbf{x_1} \right> \mathbf{x_1} + \left< \mathbf{y} , \mathbf{x_2} \right> \mathbf{x_2} + \cdots + \left< \mathbf{y} , \mathbf{x_m} \right> \mathbf{x_m} $, $ \mathbf{y_2} = \mathbf{y} - \mathbf{y_1} $
이때 $ \left< \mathbf{x_i} , \mathbf{x_j} \right> = \begin{cases} 0 , & (i \neq j) \\ 1 , & (i = j) \end{cases} $ 이므로 다음과 같다.
$$ \left< \mathbf{y_2}, \mathbf{x_1} \right> = 0, \left< \mathbf{y_2}, \mathbf{x_2} \right> = 0, \cdots, \left< \mathbf{y_2}, \mathbf{x_m} \right> = 0 $$
그리고 $ \mathbf{w} \in W $ 는 $ \mathbf{w} = k_1 \mathbf{x_1} + k_2 \mathbf{x_2} + \cdots + k_m \mathbf{x_m} $ $ (k_1, k_2, \cdots, k_m \in \mathbb{R} ) $ 이므로 $ \left< \mathbf{y_2} , \mathbf{w} \right> = 0 $ 이다.
따라서 $ \mathbf{y_2} $ 는 $ W $ 의 모든 벡터와 직교한다. 이때 $ \mathbf{y_1} $ 을 $ \mathbf{y} $ 의 $ W $ 위로의 정사영 벡터라 하고, $ \mathbf{y_1} = \operatorname{proj}_{\mathbf{w}} \mathbf{y} $ 로 나타내며, $ \mathbf{y_2} $ 를 $ W $ 에 대한 $ \mathbf{y} $ 의 직교성분 벡터라 한다.
만약 $ V = \mathbb{R}^3 $ 이라면 다음과 같다.
그람-슈미트 정규직교화
만약 집합 $ S = \{\mathbf{x_1} , \mathbf{x_2}, \cdots, \mathbf{x_n} \} $ 가 $ n $ 차원 내적공간 $ V $ 의 기저이면 $ S $ 로부터 얻어지는 정규직교기저가 존재한다. 이에 대한 증명은 다음과 같다.
먼저 $ V $ 의 기저 $ S $ 로부터 정규직교집합 $ T = \{ \mathbf{y_1}, \mathbf{y_2}, \cdots, \mathbf{y_n} \} $ 을 만든다. 정규직교집합이기 때문에 $ \mathbf{y_1} = \frac{\mathbf{x_1}}{ \| \mathbf{x_1}\|} $ 이라하면 $ \mathbf{y_1} $ 은 단위벡터이다.
$ \mathbf{y_1} $ 에 의해 생성되는 부분공간 $ W_1 $ 에 대한 $ \mathbf{x_2} $ 의 직교성분 벡터를 $ \mathbf{w_2} $ 라 하면 $ \mathbf{w_2} = \mathbf{x_2} - \operatorname{proj}_\mathbf{w_1} \mathbf{x_2} = \mathbf{x_2} - \left< \mathbf{x_2}, \mathbf{y_1} \right> \mathbf{y_1} $ 이고, $ \mathbf{y_2} = \frac{\mathbf{w_2}}{\| \mathbf{w_2}\|} $ 라 하면 $ \mathbf{y_2} $ 는 단위벡터이고, $ \mathbf{y_1} $ 과 직교한다.
$ \mathbf{y_1} , \mathbf{y_2} $ 와 직교하는 벡터를 만들기 위하여 $ \{ \mathbf{y_1} , \mathbf{y_2} \} $ 에 의하여 생성되는 부분공간 $ W_2 $ 에 대한 $ \mathbf{x_3} $ 의 직교성분 벡터를 $ \mathbf{w_3} $ 이라 하면 $ \mathbf{w_3} = \mathbf{x_3} - \operatorname{proj}_\mathbf{w_2} \mathbf{x_3} = \mathbf{x_3} - \left< \mathbf{x_3}, \mathbf{y_1} \right> \mathbf{y_1} - \left< \mathbf{x_3}, \mathbf{y_2} \right> \mathbf{y_2} $ 이고, $ \mathbf{y_3} = \frac{\mathbf{w_3}}{\| \mathbf{w_3} \|} $ 라 하면 $ \mathbf{y_3} $ 는 단위벡터이고, $ \mathbf{y_1} , \mathbf{y_3} $ 와 직교한다.
같은 방법으로 $ \mathbf{y_4}, \cdots, \mathbf{y_n} $ 을 만들 수 있다. 즉 다음이 성립한다.
$ \mathbf{w_i} = \mathbf{x_i} - \operatorname{proj}_\mathbf{w_{i-1}} \mathbf{x_i} = \mathbf{x_i} - \left< \mathbf{x_i} , \mathbf{y_1} \right> \mathbf{y_1} - \left< \mathbf{x_i} , \mathbf{y_2} \right> \mathbf{y_2} - \cdots - \left< \mathbf{x_i} , \mathbf{y_{i-1}} \right> \mathbf{y_{i-1}} $, $ \left( \mathbf{y_i} = \dfrac{\mathbf{w_i}}{\| \mathbf{w_i} \|}, \quad i = 1, 2, \cdots, n \right) $
따라서 $ T = \{ \mathbf{y_1}, \mathbf{y_2}, \cdots, \mathbf{y_n} \} $ 은 $ V $ 의 정규직교집합이고, 일차독립이기에 정규직교기저이다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] 선형변환(linear transformation)과 그 성질 및 핵(kernel), 상(image), 차원(dimension) (0) | 2024.11.20 |
|---|---|
| [Linear Algebra] 곡선적합(curve fitting) 및 최소제곱법(least square method) (0) | 2024.11.18 |
| [Linear Algebra] 내적공간(inner product space) (0) | 2024.11.14 |
| [Linear Algebra] 좌표벡터(coordinates vector)와 전이행렬(transition matrix) (0) | 2024.11.13 |
| [Linear Algebra] 행공간(row space)과 열공간(column space) (0) | 2024.11.08 |