확률값 계산
$ P (a \leq X \leq b ) $ 의 값을 구하기 위해 먼저 $ X $ 를 표준화하고 그 후에 확률을 계산하면 다음과 같이 나타낼 수 있다. 이때 $ \varphi $ 는 표준정규분포의 확률밀도함수이다.
$$ P(a \leq X \leq b) = P\left( \dfrac{a-\mu}{\sigma} \leq \dfrac{X-\mu}{\sigma} \leq \dfrac{b-\mu}{\sigma} \right) $$
$$ = P(z_a \leq Z \leq z_b) $$
$$ = \int_{-\infty}^{z_b} \varphi(t) dt - \int_{-\infty}^{z_a} \varphi(t) dt $$
$$ = \Phi(z_b) - \Phi(z_a) $$
또한 확률밀도함수의 정의를 생각한다면 다음이 성립한다.
$$ \Phi(z) = 1 - \Phi(-z) $$
수치를 계산하기 위해서는 확률밀도함수에 해당 값을 대입하여 계산해주는 통계 프로그램에 입력하여 구하거나 확률표를 이용한다.
표준정규분포표 (Standard Normal Table)
표준정규분포표는 위와 같이 생겼으며 표준정규분포에 대한 누적확률을 제공한다. 그림을 통해서 알 수 있듯이 $ z $ 가 특정 값일 때 누적확률을 표에서 찾을 수 있다. 즉 $ \Phi(z) $ 를 제공한다. 단 반대로 $ 1 - \Phi(z) $ 를 제공하는 표도 있으니 표를 활용할 때는 잘 확인하고 활용해야 한다.
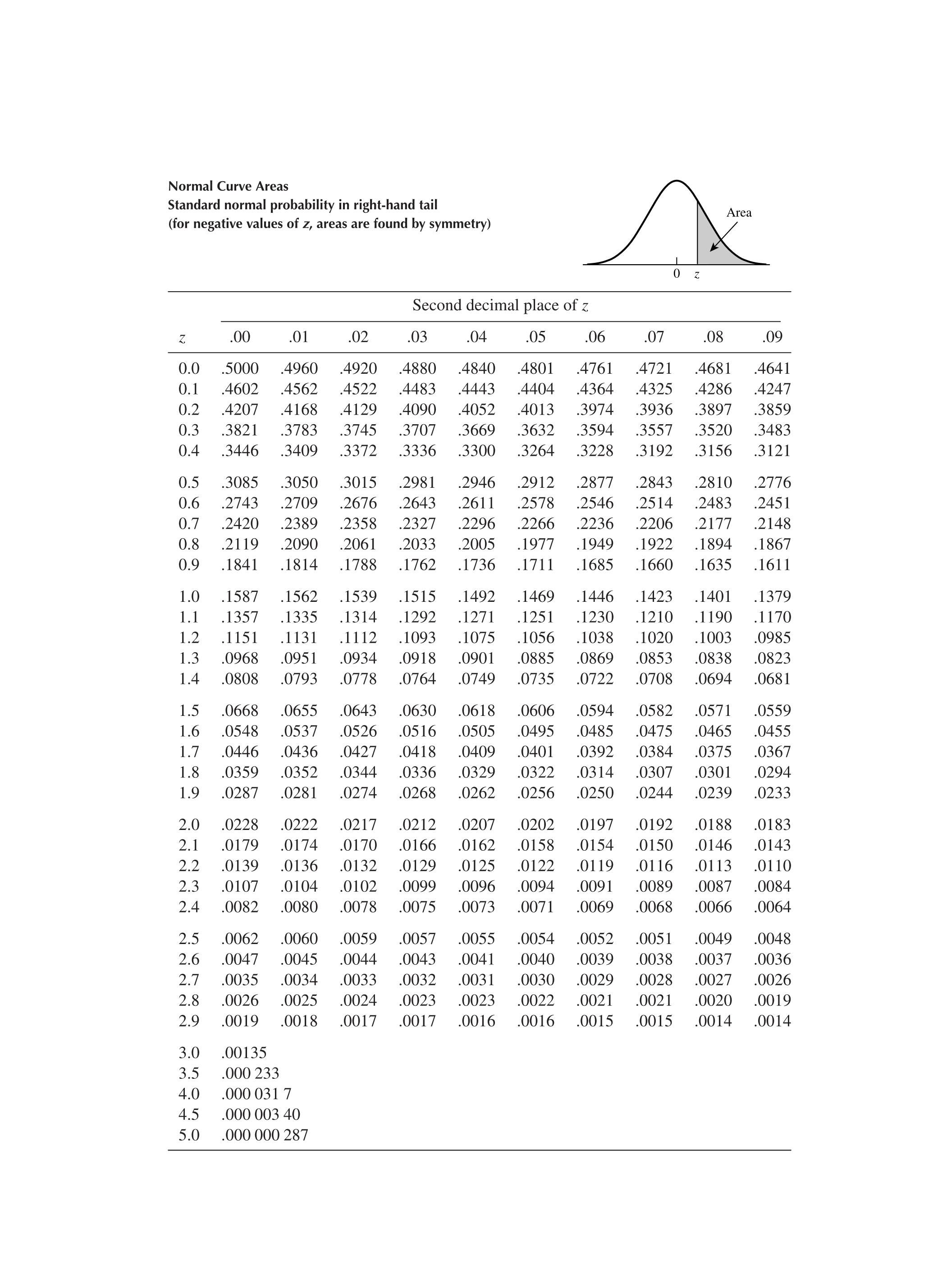
이 경우 앞서 말한 $ \Phi(z) = 1 - \Phi(-z) $ 라는 것을 이용한다.
확률값을 아는 상태로 $ z $ 값을 찾고자 한다면 반대로 확률을 표준정규분포표에서 찾고, $ z $ 값을 찾으면 된다.
경험 법칙 (Empirical Rule)
정규분포의 특징을 생각해보면 좌우대칭에 $ \mu $ 와 $ \sigma $ 에 따라 확률밀도함수의 형태가 달라졌다. 이를 통해서 기댓값이자 확률밀도함수의 중앙인 $ \mu $ 에서 좌우로 얼마나 떨어져있는지에 따라 대략적인 적분값, 즉 확률을 알 수 있다.
$ \mu $ 에서 좌우로 $ \sigma $ 만큼 떨어져 있는 구간의 적분값은 $ 0.68 $ 이고, $ 2 \sigma $ 만큼 떨어진 구간은 $ 0.95 $, $ 3\sigma $ 만큼 떨어진 구간은 $ 0.997 $ 이다. 기본적으로 기억하고 있다면 대략적인 확률을 계산하는 데에 도움이 된다.

