정의
함수 $ f(x) $ 가 존재할 때 임의의 양수 $ \epsilon $ 만큼 주어진 치역 범위 $$ \left| f(x) - L \right| < \epsilon $$ 안에 공역을 온전히 대응시킬 수있는 해당 정의역 $$ 0 < \left| x - a \right| < \delta $$ 및 정의역 범위 $ \delta $ 가 $ \epsilon $ 값과 무관하게 항상 존재한다면 $ x \to a $ 일 때 함수 $ f(x) $ 의 극한값을 $ L $ 이라고 정의한다. 이때 함수 $ f(x) $ 는 $ x \to a $ 에서 $ L $ 에 수렴한다고 하며, $$ \lim_{x \to a}{f(x)} = L $$ 로 표현한다.
설명
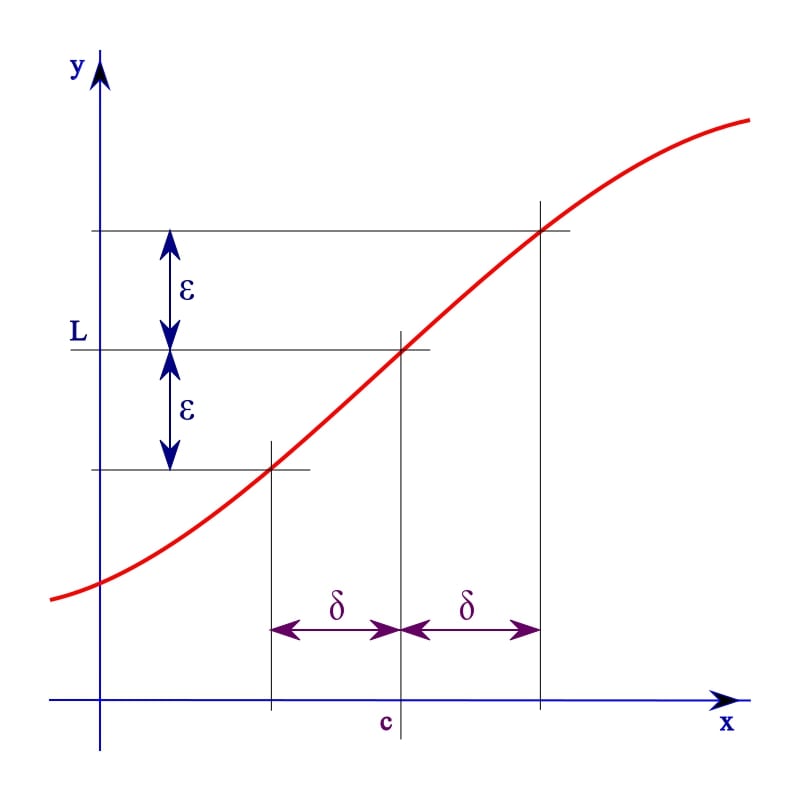
$ f(x) $ 의 값과 $ L $ 의 값의 차이가 임의의 양수 $ \epsilon $ 미만이 되도록 하자. 즉, $ \epsilon $ 이 한없이 작아진다면, 편의상 $ f(x) $ 가 $ L $ 에 한없이 가까워진다고 할 수 있다. 또한, $ x $ 와 $ c $ 의 차가 양수이면서 $ \delta $ 보다 작다고 가정하자. 즉, $ \delta $ 가 한없이 작아진다면 $ x $ 가 $ c $ 에 한없이 가까워진다고 할 수 있다.
이러한 상황에서 함수 $ f(x) $ 의 치역과 정의역의 관계를 다음과 같이 정리할 수 있다. $ f(x) $ 가 $ L $ 에 가까워지는 정도는 $ \left| f(x) - L \right| < \epsilon $ 로 표현되며, 이는 함수 값의 범위에 대한 제약을 의미한다. 반면, $ x $ 가 $ c $ 에 가까워지는 정도는 $ 0 < \left| x - c \right| < \delta $ 로 표현되며, 이는 정의역의 범위를 나타낸다.
이제, $ \epsilon $ 이 아무리 작더라도 항상 이에 대응하는 $ \delta $ 가 존재할 수 있다고 하자. 즉, $ f(x) $ 가 $ L $ 에 한없이 가까워지기 위해서는, $ x $ 가 $ c $ 에 충분히 가까워지면 된다. 이를 수학적으로 표현하면, $ \forall \epsilon > 0 $ 에 대해 $ \exists \delta > 0 $ 이 존재하여 $ 0 < \left| x - c \right| < \delta $ 일 때 $ \left| f(x) - L \right| < \epsilon $ 이 성립해야 한다. 이러한 관계가 성립한다면, 우리는 $ x \to c $ 일 때 $ f(x) \to L $ 이라고 말할 수 있다. 이를 함수의 극한이라 하며, 일반적으로 다음과 같은 기호로 표현된다.
$$ \lim_{x \to c}{f(x)} = L $$
즉, 함수 $ f(x) $ 가 $ x = c $ 에서 $ L $ 로 수렴한다고 정의한다.
예제
$ \lim_{x \to 2}{\dfrac{2x^3 - 3x - 2}{x-2}} = 5 $ 를 증명하자.
- 예비 분석
임의의 양수 $ \epsilon $ 에 대하여 $ 0 < \left| x - 2 \right| < \delta \Longrightarrow \left| \dfrac{2x^3 - 3x - 2}{x-2} \right| < \epsilon $ 인 $ \delta $ 를 찾아야 한다. $ x \neq 2 $ 인 $ x $ 에 대하여 $$ \left| \dfrac{(2x+1)(x-2)}{x-2} -5 \right| = \left| 2x + 1 - 5 \right| = \left| 2 (x-2) \right| = 2 \left| x-2 \right| < \epsilon $$ $$ \left| x-2 \right| < \dfrac{\epsilon}{2} $$ 이것으로 $ \delta = \dfrac{\epsilon}{2} $ 이면 된다는 것을 알 수 있다.
- 증명
$ \epsilon > 0 $ 을 임의의 양수라 할 때 $ \delta = \dfrac{\epsilon}{2} $ 이라 하면 $ 0 < \left| x-2 \right| < \delta $ 인 $ x $ 에 대하여 $$ \left| \dfrac{2x^3 - 3x - 2}{x-2} - 5 \right| = \left| \dfrac{(2x+1)(x-2)}{x-2} - 5 \right| = 2 \left| x - 2 \right| < 2 \delta = \epsilon \quad \blacksquare $$
'Mathematics > Calculus' 카테고리의 다른 글
| [Calculus] 도함수의 특이점 (0) | 2024.09.08 |
|---|---|
| [Calculus] 도함수(derivative)의 성질 및 삼각함수의 도함수 (0) | 2024.09.04 |
정의
함수 $ f(x) $ 가 존재할 때 임의의 양수 $ \epsilon $ 만큼 주어진 치역 범위 $$ \left| f(x) - L \right| < \epsilon $$ 안에 공역을 온전히 대응시킬 수있는 해당 정의역 $$ 0 < \left| x - a \right| < \delta $$ 및 정의역 범위 $ \delta $ 가 $ \epsilon $ 값과 무관하게 항상 존재한다면 $ x \to a $ 일 때 함수 $ f(x) $ 의 극한값을 $ L $ 이라고 정의한다. 이때 함수 $ f(x) $ 는 $ x \to a $ 에서 $ L $ 에 수렴한다고 하며, $$ \lim_{x \to a}{f(x)} = L $$ 로 표현한다.
설명

$ f(x) $ 의 값과 $ L $ 의 값의 차이가 임의의 양수 $ \epsilon $ 미만이 되도록 하자. 즉, $ \epsilon $ 이 한없이 작아진다면, 편의상 $ f(x) $ 가 $ L $ 에 한없이 가까워진다고 할 수 있다. 또한, $ x $ 와 $ c $ 의 차가 양수이면서 $ \delta $ 보다 작다고 가정하자. 즉, $ \delta $ 가 한없이 작아진다면 $ x $ 가 $ c $ 에 한없이 가까워진다고 할 수 있다.
이러한 상황에서 함수 $ f(x) $ 의 치역과 정의역의 관계를 다음과 같이 정리할 수 있다. $ f(x) $ 가 $ L $ 에 가까워지는 정도는 $ \left| f(x) - L \right| < \epsilon $ 로 표현되며, 이는 함수 값의 범위에 대한 제약을 의미한다. 반면, $ x $ 가 $ c $ 에 가까워지는 정도는 $ 0 < \left| x - c \right| < \delta $ 로 표현되며, 이는 정의역의 범위를 나타낸다.
이제, $ \epsilon $ 이 아무리 작더라도 항상 이에 대응하는 $ \delta $ 가 존재할 수 있다고 하자. 즉, $ f(x) $ 가 $ L $ 에 한없이 가까워지기 위해서는, $ x $ 가 $ c $ 에 충분히 가까워지면 된다. 이를 수학적으로 표현하면, $ \forall \epsilon > 0 $ 에 대해 $ \exists \delta > 0 $ 이 존재하여 $ 0 < \left| x - c \right| < \delta $ 일 때 $ \left| f(x) - L \right| < \epsilon $ 이 성립해야 한다. 이러한 관계가 성립한다면, 우리는 $ x \to c $ 일 때 $ f(x) \to L $ 이라고 말할 수 있다. 이를 함수의 극한이라 하며, 일반적으로 다음과 같은 기호로 표현된다.
$$ \lim_{x \to c}{f(x)} = L $$
즉, 함수 $ f(x) $ 가 $ x = c $ 에서 $ L $ 로 수렴한다고 정의한다.
예제
$ \lim_{x \to 2}{\dfrac{2x^3 - 3x - 2}{x-2}} = 5 $ 를 증명하자.
- 예비 분석
임의의 양수 $ \epsilon $ 에 대하여 $ 0 < \left| x - 2 \right| < \delta \Longrightarrow \left| \dfrac{2x^3 - 3x - 2}{x-2} \right| < \epsilon $ 인 $ \delta $ 를 찾아야 한다. $ x \neq 2 $ 인 $ x $ 에 대하여 $$ \left| \dfrac{(2x+1)(x-2)}{x-2} -5 \right| = \left| 2x + 1 - 5 \right| = \left| 2 (x-2) \right| = 2 \left| x-2 \right| < \epsilon $$ $$ \left| x-2 \right| < \dfrac{\epsilon}{2} $$ 이것으로 $ \delta = \dfrac{\epsilon}{2} $ 이면 된다는 것을 알 수 있다.
- 증명
$ \epsilon > 0 $ 을 임의의 양수라 할 때 $ \delta = \dfrac{\epsilon}{2} $ 이라 하면 $ 0 < \left| x-2 \right| < \delta $ 인 $ x $ 에 대하여 $$ \left| \dfrac{2x^3 - 3x - 2}{x-2} - 5 \right| = \left| \dfrac{(2x+1)(x-2)}{x-2} - 5 \right| = 2 \left| x - 2 \right| < 2 \delta = \epsilon \quad \blacksquare $$
'Mathematics > Calculus' 카테고리의 다른 글
| [Calculus] 도함수의 특이점 (0) | 2024.09.08 |
|---|---|
| [Calculus] 도함수(derivative)의 성질 및 삼각함수의 도함수 (0) | 2024.09.04 |