회귀를 통한 추세 조정 (Trend Adjustment Using Regression)
어떤 시계열이 추세가 있는 시계열(time series with a trend)이라는 것은 비정상 시계열(nonstationary time series)이라는 것이다. 이러한 시계열의 모델링 및 예측(forecasting)은 추세를 제거할 수만 있다면 크게 단순화되기에 가능하다면 추세를 제거하면 좋을 것이다.
이때 사용하기 좋은 방법 중 하나는 데이터에 대해 추세 성분을 설명하는 회귀 모델을 적합시킨 후, 그 추세 성분을 원 시계열(original time serise)에서 빼내서 추세가 제거된 잔차(residuals)를 얻는 것이다.
회귀식을 이용하여 추세 성분을 모델링 한다면 다음 모델들을 이용할 수 있다.
- $ E(y_t ) = \beta_0 + \beta_1 t $ : 선형 추세 모델(linear trend model)
- $ E(y_t) = \beta_0 + \beta_1 t + \beta_2 t^2 $ : 이차 추세 모델(quadratic trend model)
- $ E(y_t) = \beta_0 e^{\beta_1 t} $ : 지수 추세 모델(exponential trend model)
위 모델들은 일반적으로 최소제곱법(OLS, ordinary least squares)을 이용하여 데이터에 적합된다. 어떤 모델을 선택하든 적절한 모델을 선택하여 적합된 회귀선(fitted linear line)을 얻는다면 실제 관측값에서 회귀선을 통한 예측값을 빼서 추세가 제거된 잔차(detrended residual data)를 얻을 수 있고, 이는 추세가 제거되었기에 정상 시계열일 가능성이 높다.
예를 들어 위 데이터는 미국의 연간 블루치즈 및 고르곤졸라 치즈 생산량과 그에 따른 선형회귀선을 나타낸 것이다. 이 시계열 데이터가 선형적 증가 추세(positive linear trend)를 보이는 것은 명확해 보인다.

이제 회귀선을 이용하여 추세를 제거한 모델의 잔차(residuals)를 아래와 같이 그래프로 확인하자.

(a)와 (c)를 통해서 잔차들의 분포가 정규분포와 유사하다는 것을 알 수 있지만, (b)와 (d)를 통해서는 잔차의 분산이 일정하지 않다는 것을 알 수 있다. 따라서 (d)와 같은 추세가 제거된 그래프를 얻는 것에는 성공했지만, 완전한 정상 시계열(stationary time series)을 얻는 것에는 실패했다는 것을 알 수 있다.
차분을 통한 추세 조정 (Trend Adjustment Using Differencing)
데이터들 자체가 아니라 데이터간 차이를 통해서 새로운 데이터를 얻을 수 있다. 이를 시계열에 적용하면, 오늘 데이터 값과 내일 데이터 값 자체를 비교하는 것이 아니라 오늘과 내일의 데이터 값의 차이를 데이터로 만들어 사용할 수 있을 것이다. 이를 차분이라 한다.
이렇게 차분을 하면 원 데이터, 여기서는 원 시계열에서는 증가 추세를 보이던 데이터를 증가 수준에 대한 데이터로 만들어서 증가 추세를 제거, 혹은 억제할 수 있다.
차분은 원 시계열(original time series)에 후방차분 연산자(difference operator) $ \triangledown $ 을 사용하여 계산하고, 이를 통해 새로운 시계열을 얻는다. $ t $ 시간에 대한 새로운 데이터 $ x_t $ 는 다음과 같다.
$$ x_t = y_t - y_{t-1} = \triangledown y_t $$
차분 연산을 표현하는 또 다른 방법은 후방이동 연산자(backshift operator) $ B $ 를 이용하는 것이다.
$$ B y_t = y_{t-1} $$
이를 이용하면 차분을 다음과 같이 나타낼 수 있다.
$$ x_t = (1-B)y_t = \triangledown y_t = y_t - y_{t-1} $$
이러한 차분을 추세(trend)가 제거될 때까지 연속적으로 수행할 수 있다. 예를 들어 두번째 차분은 다음과 같다.
$$ x_t = \triangledown^2 y_t = \triangledown (\triangledown y_t) = (1-B)^2 y_t = (1-2B+B^2) = y_t - 2y_{t-1} + y_{t-2} $$
일반적으로 후방이동 연산자 $ B $ 와 후방차분 연산자 $ \triangledown $ 의 거듭제곱은 다음과 같이 정의된다.
$$ B^d y_t = y_{t-d} , \qquad \triangledown^d = (1-B)^d $$
이렇게 차분을 이용하는 것은 회귀로 적합시키는 것에 비해 몇가지 장점을 가진다. 먼저 추정해야할 매개변수(parameter)가 없기 때문에 더 간결한(parsimonious) 방법이다. 또 다른 장점은 회귀선 적합을 통해 추세를 제거하는 방식은 추세가 시계열 전 구간에 걸쳐 고정되어 있다는 가정(assumption of fixed trend)을 전제로 하기 때문에 추세 성분(trend component)이 한 번 추정되면 결정론적 성격(deterministic nature)을 가지게 된다. 반면 차분은 시간에 따라 변화하는 추세(component that changes through time)를 허용하기에 더 유연하다.
$1$차 차분(first difference)은 평균의 변화(change in the mean)에 영향을 주는 추세를, $2$차 차분(second difference)은 기울기의 변화(change in the slope)를 반영한다. 실제로는 한두번의 차분이면 내재된 추세를 제거하는 데에 충분하다.
회귀를 이용했던 미국 블루 및 고르곤졸라 치즈 판매량 데이터에 $1$차 차분을 적용하여 보면 아래와 같다.

추세가 제거되고, 보기에는 정상 시계열(stationary time series)에 가깝게 변하였다. 잔차(residuals)에 대한 것을 확인하면 아래와 같다.

앞선 회귀를 사용할 때와 비슷하게 (a)와 (c)를 통해 잔차의 정규성을 볼 수 있는데, 다른 것은 (b)와 (d)에 나타나는 잔차의 분산이다. 앞선 회귀를 이용했을 때와 달리 훨씬 분산이 일정한 것을 알 수 있다.
차분을 통한 계절성 조정 (Seasonal Adjustment Using Differencing)
차분은 추세(trend)를 제거하는 데에도 사용하였지만, 계절성(seasonality)을 조정하는 데에도 사용 가능하다. 시차(lag) $ d $ 의 계절 차분 연산자(seasonal difference operator)를 다음과 같이 정의하자.
$$ \triangledown_d y_t = (1-B^d) = y_t - y_{t-d} $$
그리고 이를 활용하여 계설성을 제거할 수 있다. 예를 들어 월별 데이터에 연간 계절성이 있다면, $ d = 12$ 로하여 차분하면된다.
$ \triangledown_{12} y_t = (1-B^{12}) = y_t - y_{t-12} $
이렇게 하면 각 월에 따른 차이로 데이터가 나오기 때문에 계절성을 제거할 수 있다.
만약 추세와 계절성이 동시에 존재한다면 이들을 제거하기 위해 차분을 순차적으로 수행할 수 있다. 먼저 계절 차분을 통해 계절성을 제거하고, 일반 차분 연산자를 이용하여 한 번 또는 여러 번 차분함으로써 추세를 제거하면 된다.
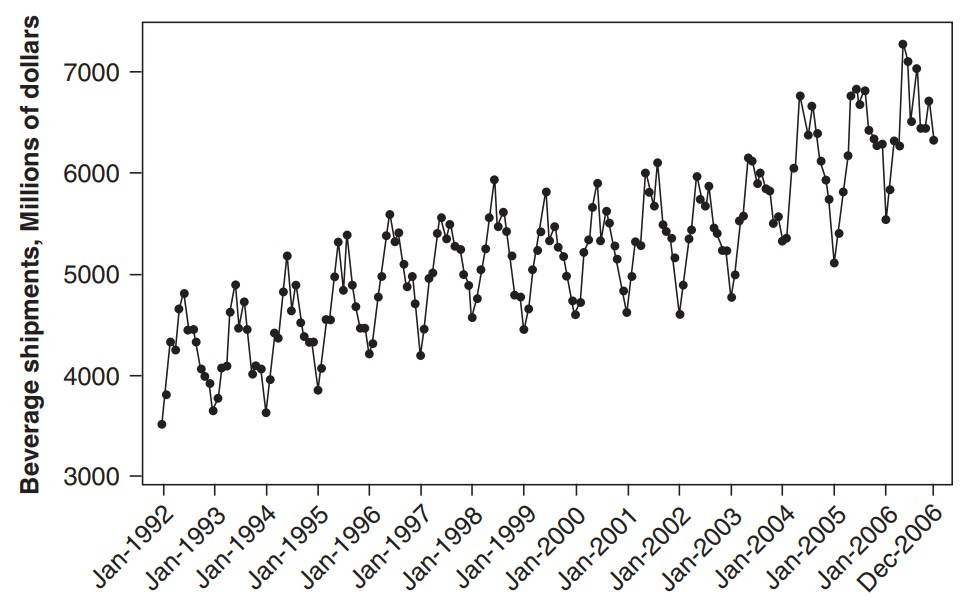
아래 데이터는 계절성과 추세가 모두 존재하는 음료 출하량 데이터이다.
이제 이 데이터에 계절적 차분을 통해 아래와 (a)와 같이 만들어주었고, $2$차 차분(second difference)하여 (b)와 같이 만들어주었다.
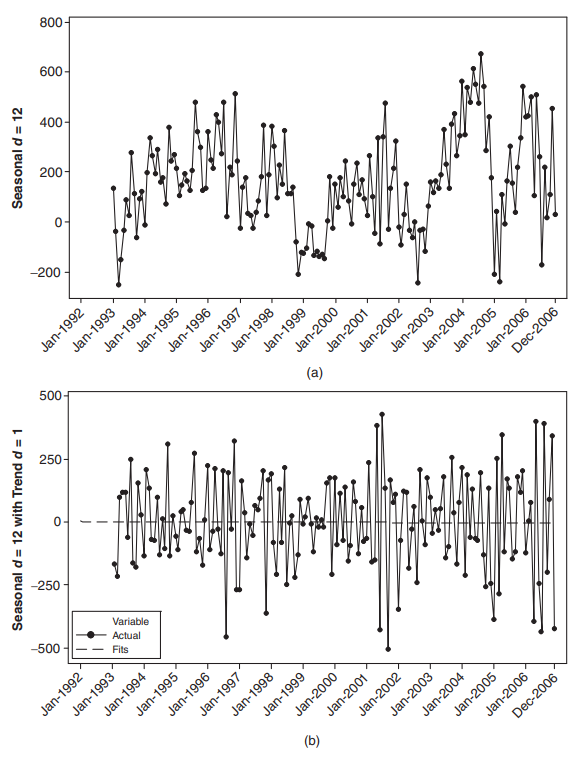
(a)를 확인하면 계절성이 제거된 모습을 볼 수 있고, (b)를 확인하면 평균과 분산이 일정한 정상 시계열(stationary time series)로 보인다. 즉 차분을 통해 추세와 계절성을 제거하였다.
회귀를 통한 계절성 조정 (Seasonal Adjustment Using Regression)
시계열 데이터가 특정 주기성, 즉 계절성(seasonality)을 가지는 경우 다음과 같은 회귀 모델을 이용해 계절 효과를 제거할 수 있다.
$$ E(y_t) = \beta_0 + \beta_1 \sin \left( \frac{2 \pi}{d} t \right) + \beta_2 \cos \left( \frac{2 \pi}{d} t \right) $$
여기서 $ d $ 는 계절 주기이다. 예를 들어 월별 데이터에서 계절성이 나타난다면 $ d = 12 $ 이다.
$ E(y_t) = \beta \sin \omega (t + \theta) $
위 경우를 생각해보자. 여기서 $ \beta $ 는 진폭(amplitude), $ \theta $ 는 위상각 또는 원점, $ \omega $ 는 주기 또는 사이클의 길이이다.
또한 삼각함수 항등식 $ \sin (u + v) = \cos u \sin v + \sin u \cos v $ 를 생각하자. 그렇다면 다음이 성립한다.
$ E(y_t) = \beta \sin ( \omega(t + \theta)) $
$ = \beta \cos(\omega \theta) \sin (\omega t) + \beta \sin(\omega \theta) \cos (\omega t) $
$ = \beta_1 \sin (\omega t) + \beta_2 \cos (\omega t) $
여기서 $ \beta_1 = \beta \cos (\omega \theta) $ 이고, $ \beta_2 = \beta \sin (\omega \theta) $ 이다.
이때 $ \omega = 2\pi / 12 $ 로 설정하고 절편 항 $ \beta_0 $ 를 추가하면 다음과 같다.
$ E(y_t) = \beta_0 + \beta_1 \sin \left( \frac{2 \pi}{d} t \right) + \beta_2 \cos \left( \frac{2 \pi}{d} t \right) $
여기서 월별이 아니라 주별로 보고 관측되는 연간 계절 패턴을 보고 싶다면 $ \omega = 2\pi /52 $ 로 설정하면 되고, 분기별이라면 $ \omega = 2\pi / 4 $ 로 설정하면 된다.
즉 이 모델은 매우 유연하다.
만약 계절 패턴이 단순한 사인, 코사인 한 쌍으로 표현되지 않는다면 추가적인 조화(harmonics)을 고려하여 더 정확한 모델을 구축할 수도 있다. 즉 회귀계수를 늘려서 그 정확성을 늘릴수도 있다.
예를 들어 월별 데이터와 1년 주기의 계절성을 가정했을 때, 기본 빈도(frequency)와 추가 세 개의 조화를 고려하는 경우 아래와 같이 일반적인 모형을 만들 수 있다.
$$ E(y_t) = \beta_0 + \sum_{j=1}^4 \left( \beta_j \sin \frac{2 \pi j}{12} t + \beta_{4+j} \cos \frac{2\pi j}{12} t \right) $$
고전적 방법 (Classical Approach)
시계열 데이터의 추세 및 계절성을 분해하는 데에는 이른바 고전적 방식도 존재한다. 계절성을 $ S_t $, 추세를 $ T_t $, 무작위 잔차를 $ \epsilon_t $ 라 할 때 다음과 같이 수학적 모형으로 나타낸다.
$$ y_t = f(S_t, T_t, \epsilon_t)$$
그리고 다시 이는 일반적으로 두 가지로 나뉜다.
- $ y_t = S_t + T_t + \epsilon_t $ : 가법 모형(additive model)
- $ y_t = S_t \cdot T_t \cdot \epsilon_t $ : 승법 모형(multiplicative model)
가법 모형은 추세 형태가 선형적이거나 완만할 때 사용하면 좋고, 계절 변동의 진폭이 시계열의 평균 수준에 따라 증가하거나 감소하면 승법 모형이 더 적절하다. 참고로 승법 모형은 로그를 취해주면 가법 모형처럼 다룰 수 있다.
두 모형 모두 사용은 비슷하다. 우선 먼저 추세를 분리해야 한다. 추세는 $ T_t = \beta_0 + \beta_1 t $ 와 같이 간단한 선형 모델을 사용하여 추정할 수도 있고, 이동평균(moving averages)을 사용할 수도 있다. 차분도 사용할 수는 있으나 일반적으로 고전적 방법에서는 잘 사용되지 않는다.
추세를 찾았다면 이제 원 시계열(original time series)에서 추세를 제거하면 된다. 가법 모형이라면 빼주면 될 것이고, 승법 모형이라면 나눠주면 될 것이다. 승법 모형이 로그를 취해준 상태라면 가법 모형처럼 다루면 된다.
$$ y_t - T_t = S_t + \epsilon_t \qquad \text{ or } \qquad \frac{y_t}{T_t} = S_t \cdot \epsilon_t $$
이제 계절성을 분리해야 한다. 예를 들어 추세가 제거된 월별 데이터가 있다고 가정하자. 이제 각 달에 해당하는 값들만 모아서 평균을 낸다. 그렇다면 그 값이 각 달의 계절 지수(seasonal index)가 된다. 이제 다시 계절 지수를 통해 계절성을 제거해주면 다음과 같이 잔차(residual)를 추정할 수 있다.
$$ \epsilon_t = y_t - T_t - S_t \qquad \text{ or } \qquad \epsilon_t = \frac{y_t}{T_t \cdot S_t} $$
이렇게 잔차를 구했을 때 이 잔차의 분산이 일정하다면 이렇게 추세와 계절성이 제거된 데이터는 정상 시계열(stationary time series)이다.
주의점
원래 단위의 시계열 $y_t $ 와 모델이 예측한 값의 차이도 중요한데, 이때 주의해야 할 것은 원래 단위로 예측값을 산출하기 위해서는 추세나 계절 효과를 제거하기 위해 수행했던 변환(transformations)이나 차분(differencing) 조정을 되돌려야 한다. 특히 로그 변환이 적용되었다면 지수로 바꿔주어야 한다.
예를 들어 원래 시계열 $ y_t $ 에 대해 로그를 취해 $ x_t = \ln y_t $ 로 변환하여 예측했다면 $ T $ 시점에서의 $ T + \tau $ 에 대한 예측 결과 $ \hat{x}_{T+\tau}(T) $ 를 그대로 사용하면 안되고, $ \hat{y}_{T+\tau}(T) = \exp [ \hat{x}_{T+\tau}(T)] $ 로 사용해야 한다.
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [Time Series Analysis] 예측 모델(forecasting model) 선택(Choosing) (0) | 2025.03.26 |
|---|---|
| [Time Series Analysis] 예측 모델(forecasting model) 평가(evaluation) (0) | 2025.03.23 |
| [Time Series Analysis] 멱변환(power transformation)을 통한 데이터 변환(data transformation) (0) | 2025.03.20 |
| [Time Series Analysis] 변이도(variogram) (0) | 2025.03.15 |
| [Time Series Analysis] 시계열 자료의 정상성(stationarity) (0) | 2025.03.15 |
회귀를 통한 추세 조정 (Trend Adjustment Using Regression)
어떤 시계열이 추세가 있는 시계열(time series with a trend)이라는 것은 비정상 시계열(nonstationary time series)이라는 것이다. 이러한 시계열의 모델링 및 예측(forecasting)은 추세를 제거할 수만 있다면 크게 단순화되기에 가능하다면 추세를 제거하면 좋을 것이다.
이때 사용하기 좋은 방법 중 하나는 데이터에 대해 추세 성분을 설명하는 회귀 모델을 적합시킨 후, 그 추세 성분을 원 시계열(original time serise)에서 빼내서 추세가 제거된 잔차(residuals)를 얻는 것이다.
회귀식을 이용하여 추세 성분을 모델링 한다면 다음 모델들을 이용할 수 있다.
- $ E(y_t ) = \beta_0 + \beta_1 t $ : 선형 추세 모델(linear trend model)
- $ E(y_t) = \beta_0 + \beta_1 t + \beta_2 t^2 $ : 이차 추세 모델(quadratic trend model)
- $ E(y_t) = \beta_0 e^{\beta_1 t} $ : 지수 추세 모델(exponential trend model)
위 모델들은 일반적으로 최소제곱법(OLS, ordinary least squares)을 이용하여 데이터에 적합된다. 어떤 모델을 선택하든 적절한 모델을 선택하여 적합된 회귀선(fitted linear line)을 얻는다면 실제 관측값에서 회귀선을 통한 예측값을 빼서 추세가 제거된 잔차(detrended residual data)를 얻을 수 있고, 이는 추세가 제거되었기에 정상 시계열일 가능성이 높다.
예를 들어 위 데이터는 미국의 연간 블루치즈 및 고르곤졸라 치즈 생산량과 그에 따른 선형회귀선을 나타낸 것이다. 이 시계열 데이터가 선형적 증가 추세(positive linear trend)를 보이는 것은 명확해 보인다.

이제 회귀선을 이용하여 추세를 제거한 모델의 잔차(residuals)를 아래와 같이 그래프로 확인하자.

(a)와 (c)를 통해서 잔차들의 분포가 정규분포와 유사하다는 것을 알 수 있지만, (b)와 (d)를 통해서는 잔차의 분산이 일정하지 않다는 것을 알 수 있다. 따라서 (d)와 같은 추세가 제거된 그래프를 얻는 것에는 성공했지만, 완전한 정상 시계열(stationary time series)을 얻는 것에는 실패했다는 것을 알 수 있다.
차분을 통한 추세 조정 (Trend Adjustment Using Differencing)
데이터들 자체가 아니라 데이터간 차이를 통해서 새로운 데이터를 얻을 수 있다. 이를 시계열에 적용하면, 오늘 데이터 값과 내일 데이터 값 자체를 비교하는 것이 아니라 오늘과 내일의 데이터 값의 차이를 데이터로 만들어 사용할 수 있을 것이다. 이를 차분이라 한다.
이렇게 차분을 하면 원 데이터, 여기서는 원 시계열에서는 증가 추세를 보이던 데이터를 증가 수준에 대한 데이터로 만들어서 증가 추세를 제거, 혹은 억제할 수 있다.
차분은 원 시계열(original time series)에 후방차분 연산자(difference operator) $ \triangledown $ 을 사용하여 계산하고, 이를 통해 새로운 시계열을 얻는다. $ t $ 시간에 대한 새로운 데이터 $ x_t $ 는 다음과 같다.
$$ x_t = y_t - y_{t-1} = \triangledown y_t $$
차분 연산을 표현하는 또 다른 방법은 후방이동 연산자(backshift operator) $ B $ 를 이용하는 것이다.
$$ B y_t = y_{t-1} $$
이를 이용하면 차분을 다음과 같이 나타낼 수 있다.
$$ x_t = (1-B)y_t = \triangledown y_t = y_t - y_{t-1} $$
이러한 차분을 추세(trend)가 제거될 때까지 연속적으로 수행할 수 있다. 예를 들어 두번째 차분은 다음과 같다.
$$ x_t = \triangledown^2 y_t = \triangledown (\triangledown y_t) = (1-B)^2 y_t = (1-2B+B^2) = y_t - 2y_{t-1} + y_{t-2} $$
일반적으로 후방이동 연산자 $ B $ 와 후방차분 연산자 $ \triangledown $ 의 거듭제곱은 다음과 같이 정의된다.
$$ B^d y_t = y_{t-d} , \qquad \triangledown^d = (1-B)^d $$
이렇게 차분을 이용하는 것은 회귀로 적합시키는 것에 비해 몇가지 장점을 가진다. 먼저 추정해야할 매개변수(parameter)가 없기 때문에 더 간결한(parsimonious) 방법이다. 또 다른 장점은 회귀선 적합을 통해 추세를 제거하는 방식은 추세가 시계열 전 구간에 걸쳐 고정되어 있다는 가정(assumption of fixed trend)을 전제로 하기 때문에 추세 성분(trend component)이 한 번 추정되면 결정론적 성격(deterministic nature)을 가지게 된다. 반면 차분은 시간에 따라 변화하는 추세(component that changes through time)를 허용하기에 더 유연하다.
$1$차 차분(first difference)은 평균의 변화(change in the mean)에 영향을 주는 추세를, $2$차 차분(second difference)은 기울기의 변화(change in the slope)를 반영한다. 실제로는 한두번의 차분이면 내재된 추세를 제거하는 데에 충분하다.
회귀를 이용했던 미국 블루 및 고르곤졸라 치즈 판매량 데이터에 $1$차 차분을 적용하여 보면 아래와 같다.

추세가 제거되고, 보기에는 정상 시계열(stationary time series)에 가깝게 변하였다. 잔차(residuals)에 대한 것을 확인하면 아래와 같다.

앞선 회귀를 사용할 때와 비슷하게 (a)와 (c)를 통해 잔차의 정규성을 볼 수 있는데, 다른 것은 (b)와 (d)에 나타나는 잔차의 분산이다. 앞선 회귀를 이용했을 때와 달리 훨씬 분산이 일정한 것을 알 수 있다.
차분을 통한 계절성 조정 (Seasonal Adjustment Using Differencing)
차분은 추세(trend)를 제거하는 데에도 사용하였지만, 계절성(seasonality)을 조정하는 데에도 사용 가능하다. 시차(lag) $ d $ 의 계절 차분 연산자(seasonal difference operator)를 다음과 같이 정의하자.
$$ \triangledown_d y_t = (1-B^d) = y_t - y_{t-d} $$
그리고 이를 활용하여 계설성을 제거할 수 있다. 예를 들어 월별 데이터에 연간 계절성이 있다면, $ d = 12$ 로하여 차분하면된다.
$ \triangledown_{12} y_t = (1-B^{12}) = y_t - y_{t-12} $
이렇게 하면 각 월에 따른 차이로 데이터가 나오기 때문에 계절성을 제거할 수 있다.
만약 추세와 계절성이 동시에 존재한다면 이들을 제거하기 위해 차분을 순차적으로 수행할 수 있다. 먼저 계절 차분을 통해 계절성을 제거하고, 일반 차분 연산자를 이용하여 한 번 또는 여러 번 차분함으로써 추세를 제거하면 된다.
아래 데이터는 계절성과 추세가 모두 존재하는 음료 출하량 데이터이다.

이제 이 데이터에 계절적 차분을 통해 아래와 (a)와 같이 만들어주었고, $2$차 차분(second difference)하여 (b)와 같이 만들어주었다.

(a)를 확인하면 계절성이 제거된 모습을 볼 수 있고, (b)를 확인하면 평균과 분산이 일정한 정상 시계열(stationary time series)로 보인다. 즉 차분을 통해 추세와 계절성을 제거하였다.
회귀를 통한 계절성 조정 (Seasonal Adjustment Using Regression)
시계열 데이터가 특정 주기성, 즉 계절성(seasonality)을 가지는 경우 다음과 같은 회귀 모델을 이용해 계절 효과를 제거할 수 있다.
$$ E(y_t) = \beta_0 + \beta_1 \sin \left( \frac{2 \pi}{d} t \right) + \beta_2 \cos \left( \frac{2 \pi}{d} t \right) $$
여기서 $ d $ 는 계절 주기이다. 예를 들어 월별 데이터에서 계절성이 나타난다면 $ d = 12 $ 이다.
$ E(y_t) = \beta \sin \omega (t + \theta) $
위 경우를 생각해보자. 여기서 $ \beta $ 는 진폭(amplitude), $ \theta $ 는 위상각 또는 원점, $ \omega $ 는 주기 또는 사이클의 길이이다.
또한 삼각함수 항등식 $ \sin (u + v) = \cos u \sin v + \sin u \cos v $ 를 생각하자. 그렇다면 다음이 성립한다.
$ E(y_t) = \beta \sin ( \omega(t + \theta)) $
$ = \beta \cos(\omega \theta) \sin (\omega t) + \beta \sin(\omega \theta) \cos (\omega t) $
$ = \beta_1 \sin (\omega t) + \beta_2 \cos (\omega t) $
여기서 $ \beta_1 = \beta \cos (\omega \theta) $ 이고, $ \beta_2 = \beta \sin (\omega \theta) $ 이다.
이때 $ \omega = 2\pi / 12 $ 로 설정하고 절편 항 $ \beta_0 $ 를 추가하면 다음과 같다.
$ E(y_t) = \beta_0 + \beta_1 \sin \left( \frac{2 \pi}{d} t \right) + \beta_2 \cos \left( \frac{2 \pi}{d} t \right) $
여기서 월별이 아니라 주별로 보고 관측되는 연간 계절 패턴을 보고 싶다면 $ \omega = 2\pi /52 $ 로 설정하면 되고, 분기별이라면 $ \omega = 2\pi / 4 $ 로 설정하면 된다.
즉 이 모델은 매우 유연하다.
만약 계절 패턴이 단순한 사인, 코사인 한 쌍으로 표현되지 않는다면 추가적인 조화(harmonics)을 고려하여 더 정확한 모델을 구축할 수도 있다. 즉 회귀계수를 늘려서 그 정확성을 늘릴수도 있다.
예를 들어 월별 데이터와 1년 주기의 계절성을 가정했을 때, 기본 빈도(frequency)와 추가 세 개의 조화를 고려하는 경우 아래와 같이 일반적인 모형을 만들 수 있다.
$$ E(y_t) = \beta_0 + \sum_{j=1}^4 \left( \beta_j \sin \frac{2 \pi j}{12} t + \beta_{4+j} \cos \frac{2\pi j}{12} t \right) $$
고전적 방법 (Classical Approach)
시계열 데이터의 추세 및 계절성을 분해하는 데에는 이른바 고전적 방식도 존재한다. 계절성을 $ S_t $, 추세를 $ T_t $, 무작위 잔차를 $ \epsilon_t $ 라 할 때 다음과 같이 수학적 모형으로 나타낸다.
$$ y_t = f(S_t, T_t, \epsilon_t)$$
그리고 다시 이는 일반적으로 두 가지로 나뉜다.
- $ y_t = S_t + T_t + \epsilon_t $ : 가법 모형(additive model)
- $ y_t = S_t \cdot T_t \cdot \epsilon_t $ : 승법 모형(multiplicative model)
가법 모형은 추세 형태가 선형적이거나 완만할 때 사용하면 좋고, 계절 변동의 진폭이 시계열의 평균 수준에 따라 증가하거나 감소하면 승법 모형이 더 적절하다. 참고로 승법 모형은 로그를 취해주면 가법 모형처럼 다룰 수 있다.
두 모형 모두 사용은 비슷하다. 우선 먼저 추세를 분리해야 한다. 추세는 $ T_t = \beta_0 + \beta_1 t $ 와 같이 간단한 선형 모델을 사용하여 추정할 수도 있고, 이동평균(moving averages)을 사용할 수도 있다. 차분도 사용할 수는 있으나 일반적으로 고전적 방법에서는 잘 사용되지 않는다.
추세를 찾았다면 이제 원 시계열(original time series)에서 추세를 제거하면 된다. 가법 모형이라면 빼주면 될 것이고, 승법 모형이라면 나눠주면 될 것이다. 승법 모형이 로그를 취해준 상태라면 가법 모형처럼 다루면 된다.
$$ y_t - T_t = S_t + \epsilon_t \qquad \text{ or } \qquad \frac{y_t}{T_t} = S_t \cdot \epsilon_t $$
이제 계절성을 분리해야 한다. 예를 들어 추세가 제거된 월별 데이터가 있다고 가정하자. 이제 각 달에 해당하는 값들만 모아서 평균을 낸다. 그렇다면 그 값이 각 달의 계절 지수(seasonal index)가 된다. 이제 다시 계절 지수를 통해 계절성을 제거해주면 다음과 같이 잔차(residual)를 추정할 수 있다.
$$ \epsilon_t = y_t - T_t - S_t \qquad \text{ or } \qquad \epsilon_t = \frac{y_t}{T_t \cdot S_t} $$
이렇게 잔차를 구했을 때 이 잔차의 분산이 일정하다면 이렇게 추세와 계절성이 제거된 데이터는 정상 시계열(stationary time series)이다.
주의점
원래 단위의 시계열 $y_t $ 와 모델이 예측한 값의 차이도 중요한데, 이때 주의해야 할 것은 원래 단위로 예측값을 산출하기 위해서는 추세나 계절 효과를 제거하기 위해 수행했던 변환(transformations)이나 차분(differencing) 조정을 되돌려야 한다. 특히 로그 변환이 적용되었다면 지수로 바꿔주어야 한다.
예를 들어 원래 시계열 $ y_t $ 에 대해 로그를 취해 $ x_t = \ln y_t $ 로 변환하여 예측했다면 $ T $ 시점에서의 $ T + \tau $ 에 대한 예측 결과 $ \hat{x}_{T+\tau}(T) $ 를 그대로 사용하면 안되고, $ \hat{y}_{T+\tau}(T) = \exp [ \hat{x}_{T+\tau}(T)] $ 로 사용해야 한다.
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [Time Series Analysis] 예측 모델(forecasting model) 선택(Choosing) (0) | 2025.03.26 |
|---|---|
| [Time Series Analysis] 예측 모델(forecasting model) 평가(evaluation) (0) | 2025.03.23 |
| [Time Series Analysis] 멱변환(power transformation)을 통한 데이터 변환(data transformation) (0) | 2025.03.20 |
| [Time Series Analysis] 변이도(variogram) (0) | 2025.03.15 |
| [Time Series Analysis] 시계열 자료의 정상성(stationarity) (0) | 2025.03.15 |