정상성 (Stationarity)
장성성(stationarity)을 가진 시계열, 즉 정상시계열(stationary time series) 데이터는 확인하는 시점이 바뀌어도 그 자료의 특징이 변하지 않는 시계열이다. 특히 엄격한 정상성(strict stationarity)을 가정하면 그 성질이 시간의 원점 변화에 영향을 받지 않아 관측값 $ y_t, y_{t+1}, \cdots, y_{t+n} $ 의 결합확률분포(joint probability distribution)가 $ y_{t+k}, y_{t+k+1}, \cdots, y_{t+k+n} $ 과 완전히 동일(exactly same)하다. 이러한 정상성 가저은 $ n = 0 $ 일 때 $ y_t $ 의 확률분포가 모든 시간(time periods)에 대해 동일하다는 것을 의미하며 이를 $ f(y) $ 로 표현 가능하다.
정상시계열은 그래프로 그렸을 때 일정한 수준을 중심으로 변동하는 경향을 보인다. 당연하게도 확률분포가 원점 변화에 영향을 받지 않기 때문이다. 예를 들어 아래와 같은 의약품 판매 데이터는 정상시계열로 볼 수 있다.
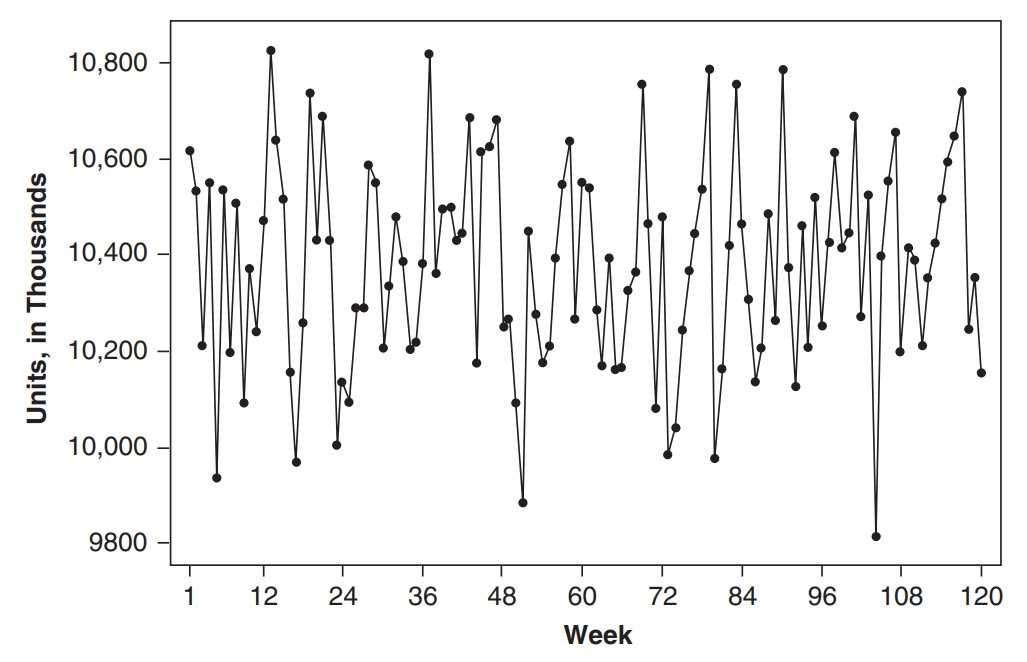
반대로 원점에 따라 변화하는, 예를 들어 아래와 같이 증가하는 시계열은 비정상시계열(non-stationary time series)이라 한다.
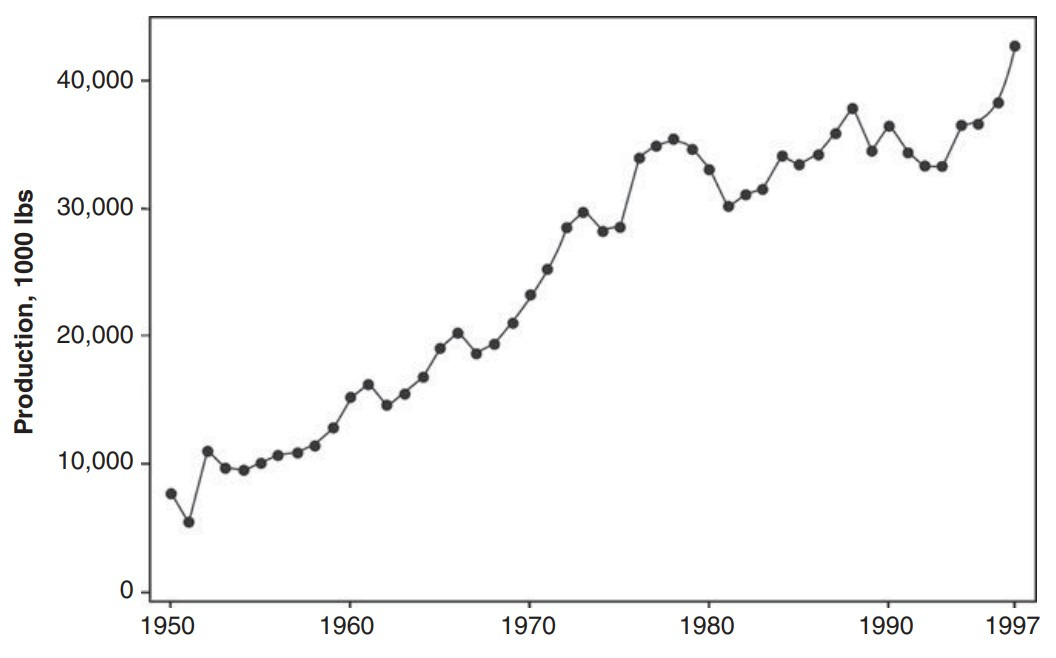
정상성은 일종의 통계적 평형(statistical equilibrium) 또는 안정성(stability)을 의미한다. 즉 정상시계열은 다음과 같은 일정한 평균과 분산을 가진다.
$$ \mu_y = E(y) = \int_{-\infty}^{\infty} y f(y) dy $$
$$ \sigma^2_y = \mathrm{Var}(y) = \int_{-\infty}^\infty (y - \mu_y)^2 f(y) dy $$
이러한 평균과 분산은 표본 데이터를 사용하여 추정하는 것이 일반적이다. 표본평균과 표본분산은 아래와 같다.
$$ \bar{y} = \hat{\mu}_y = \frac{1}{T} \sum_{i=1}^T y_t $$
$$ S^2 = \hat{\sigma}^2_y = \frac{1}{T} \sum_{t=1}^T (y_t - \bar{y})^2 $$
이때 특이하게도 일반적인 표본분산과 다르게 $ 1/(T-1) $ 이 아니라 $ 1/T $ 를 사용한다. 시계열 분석에서 흔히 사용되는 방식으로 보통 $ T $ 가 크기에 $ T-1 $ 과 차이가 크지 않다.
자기공분산 및 자기공분산 함수 (Autocovariance and Autocovariance Function)
만약 시계열이 정상시계열이라면 이는 특정 간격 $ k $ 만큼 떨어진 두 개의 관측값, 즉 $ y_t $ 와 $ y_{t+k} $ 의 결합확률분포가 모든 시간 $ t $ 에 대해 동일하다는 것을 의미하고 이러한 결합확률분포에 대해 더 알아보기 위해 동일한 간격 $ k $ 만큼 떨어진 데이터 쌍 $(y_t, y_{t+k}) $ 에 대해 산점도(scatter plot)을 그려볼 수 있다. 여기서 $ k $ 를 시차(lag)라 한다.
어떤 그래프는 아래와 같이 무상관(uncorrelated)일 수 있다. 즉 현재 시점의 값이 $k $ 시차 이후의 값, 여기서는 다음 시점의 값을 예측하는 데에 도움이 되지 않는다.
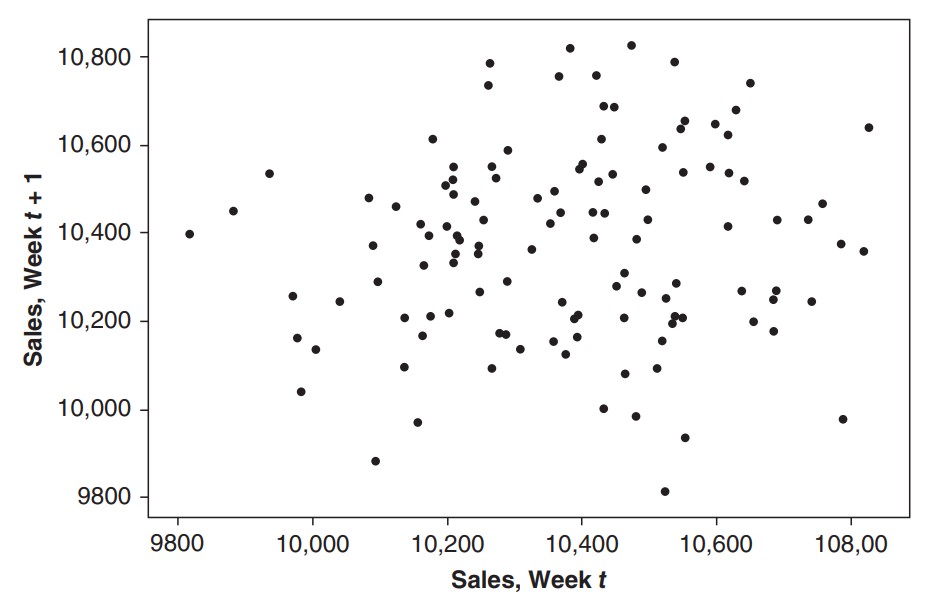
또는 아래와 같이 상관관계가 나타날 수도 있다. 아래와 같이 양의 상관관계가 나타난다는 것은 직전 값이 작다면 그 다음 값도 작고, 직전 값이 크다면 그 다음 값도 크다는 이야기이다. 즉 현재 값이 다음 값에 영향을 미친다.
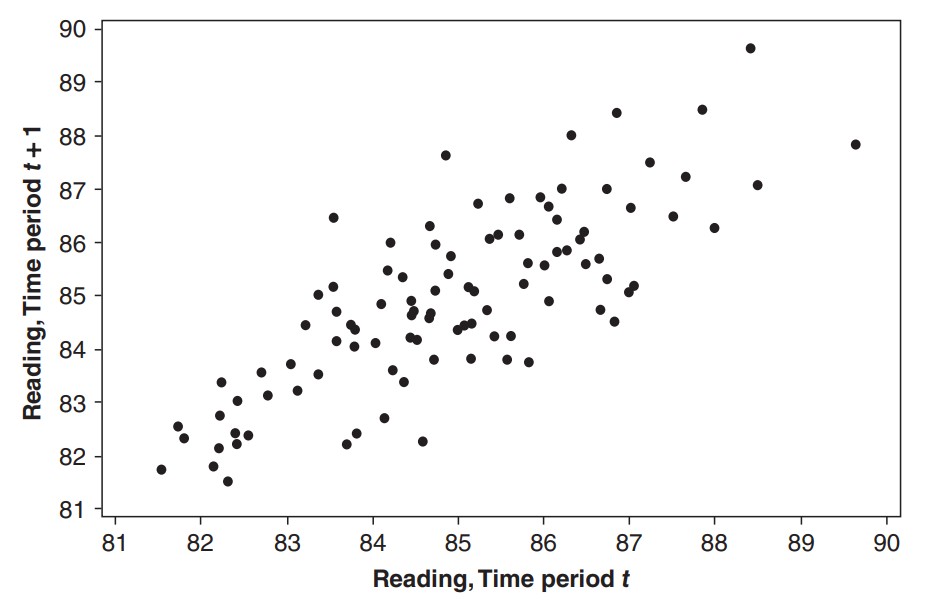
시계열의 특정 시간 $ t $ 에 대해서 다른 시간 $ t+k $ 에서의 값과의 공분산(covariance)을 시차 $ k $ 에서의 자기공분산(autocovariance at lag $ k $)이라 하고 다음과 같이 정의한다.
$$ \gamma_k = \mathrm{Cov} (y_t, y_{t+k}) = E[(y_t - \mu)(y_{t+k} - \mu)] $$
그리고 이러한 $ \gamma_k $ 값들의 집합을 자기공분산 함수(autocovariance function)라 한다. 특히 $ k = 0 $ 일 때 자기공분산은 $ \gamma_0 = \sigma_y^2 $ 으로 분산과 같다. 그리고 이는 앞서 말했듯이 정상시계열에서 항상 일정하다.
자기상관계수 및 자기상관함수 (Autocorrelation Coefficient and Autocorrelation Function)
자기상관계수는 다음과 같이 정의된다.
$$ \rho_k = \frac{E[y_t-\mu)(y_{t+k}-\mu)]}{\sqrt{E[(y_t-\mu)^2]E[(y_{t+k}-\mu)^2]}} = \frac{\mathrm{Cov}(y_t, y_{t+k})}{\mathrm{Var}(y_t)} = \frac{\gamma_k}{\gamma_0} $$
그리고 이러한 $ \rho_k $ 값들의 집합을 자기상관함수(ACF, autocorrelation function)라 한다. 정의상 $ \rho_0 = 1 $ 이고, 자기상관함수(ACF)는 시계열의 측정 단위(scale of measurement)에 독립적이므로 무차원(dimensionless) 값이다. 더불어 $ \rho_k = \rho_{-k} $ 이다. 즉 $ 0 $ 을 중심으로 대칭적이며 범위가 $ [-1, 1] $ 이라는 특성을 가진다.
약한 정상성 및 엄격한 정상성 (Weak Stationarity and Strict Stationarity)
어떤 시계열이 유한한 평균(finite mean)과 유한한 자기공분산 함수(finite autocovariance function)을 가지면 이를 2차 정상시계열(second-order stationary time series) 혹은 2차 약한 정상시계열(weakly stationary of order 2 time series)이라 한다.
만약 모든 시점에서 관측값들의 결합확률분포(joint probability distribution)가 다변량 정규분포(multivariate normal distribution)를 따른다면 해당 시계열은 엄격한 정상시계열(strictly stationary time series)이라 한다.
추정
유한한 길이를 가진 시계열 데이터 $y_1, y_2, \cdots, y_T $ 에서 자기공분산 및 자기상관함수를 추정하면 일반적으로 아래와 같은 추정값이 사용된다.
$$ c_k = \hat{\gamma}_k = \frac{1}{T} \sum_{t=1}^{T-k} (y_t - \bar{y}) (y_{t+k}-\bar{y}) , \qquad (k =0, 1, 2, \cdots, K) $$
$$ r_k = \hat{\rho}_k = \frac{c_k}{c_0} , \qquad (k = 0, 1, 2, \cdots, K) $$
신뢰할 수 있는 자기상관함수(ACF) 추정을 위해서는 최소 50개 이상의 데이터가 필요하고 최대 지연값 $ K $ 는 보통 $ K \approx T/4 $ 로 계산한다.
특정 시차(lag) $ k $ 에서 자기상관계수 $ \rho_k $ 가 $ 0 $ 인지 확인해야 하는 경우가 있다. 이를 위해 표본 자기상관계수 $ r_k $ 를 표준오차(standard error)와 비교할 수 있다. 만약 무상관(uncorrelated)이라면, 즉 모든 $ k $ 에 대해 $ \rho_k = 0 $ 이 성립한다고 가정하면 표본 자기상관계수의 분산과 표준오차는 아래와 같다.
$$ \mathrm{Var}(r_k) \approx \frac{1}{T} $$
$$ \mathrm{SE}(r_k) \approx \frac{1}{\sqrt{T}} $$
참고로 엄밀히 말하면 정상시계열에 대해서만 자기상관함수(ACF)가 정의되지만, 표본 ACF는 모든 시계열에 대해 계산 가능하다.
이제 $ r_k $ 를 통해 정상성에 대해 확인해보자. 먼저 아래와 같이 시차(lag)에 대한 ACF 값이 나타난다고 해보자.
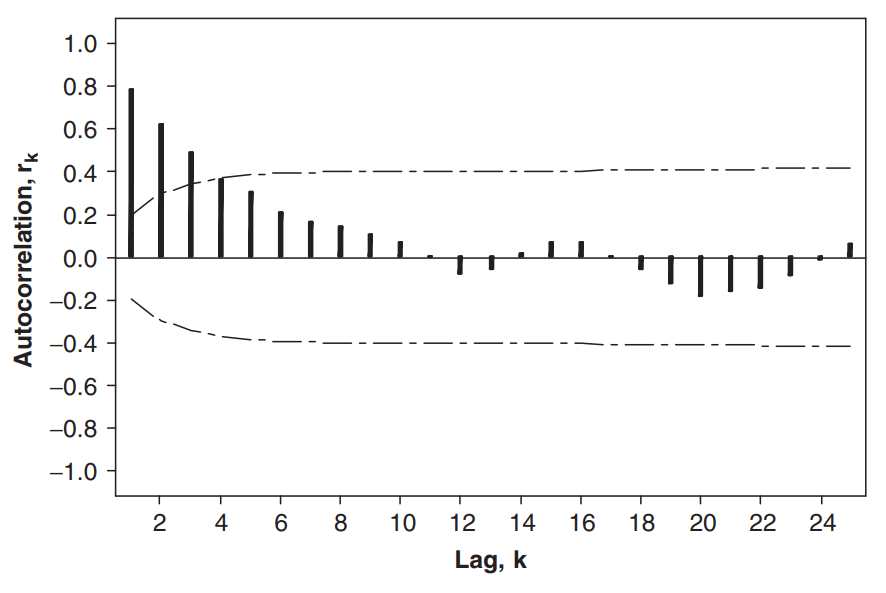
처음에는 $0.8$ 수준으로 컸지만, 일정 수준 이후 $ 0 $ 을 중심으로 사인파(sinusoidal) 패턴이 나타난다. 이러한 ACF 패턴은 정상시계열의 전형적인 특징이다. 이에 반해 일정한 평균의 무작위 시계열(time series of random values with constant mean)은 아래와 같은 패턴을 보인다.
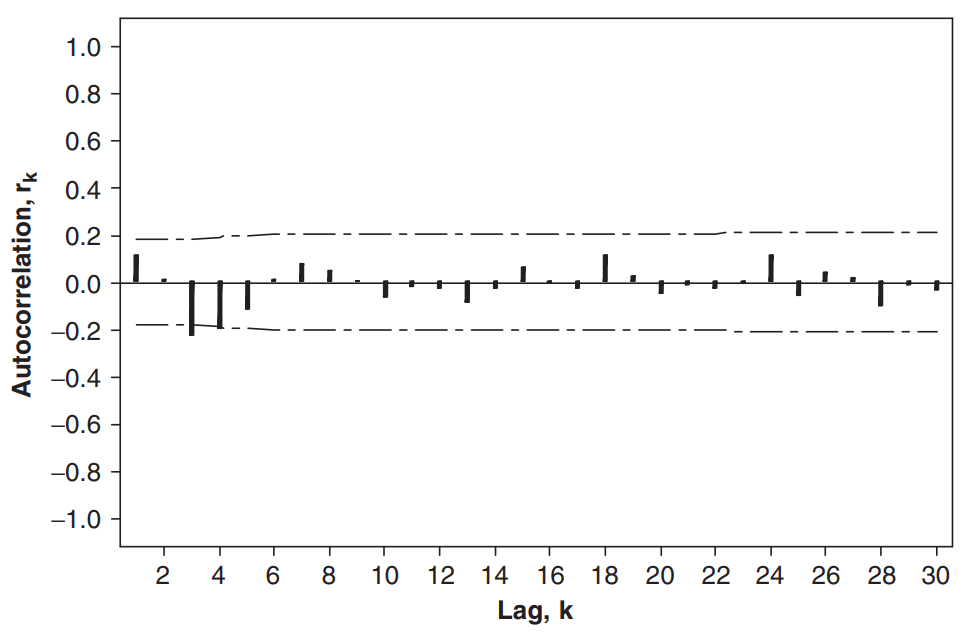
반대로 비정상시계열은 시차(lag)에 대한 ACF 값이 일반적으로 아래와 같은 패턴을 보인다.
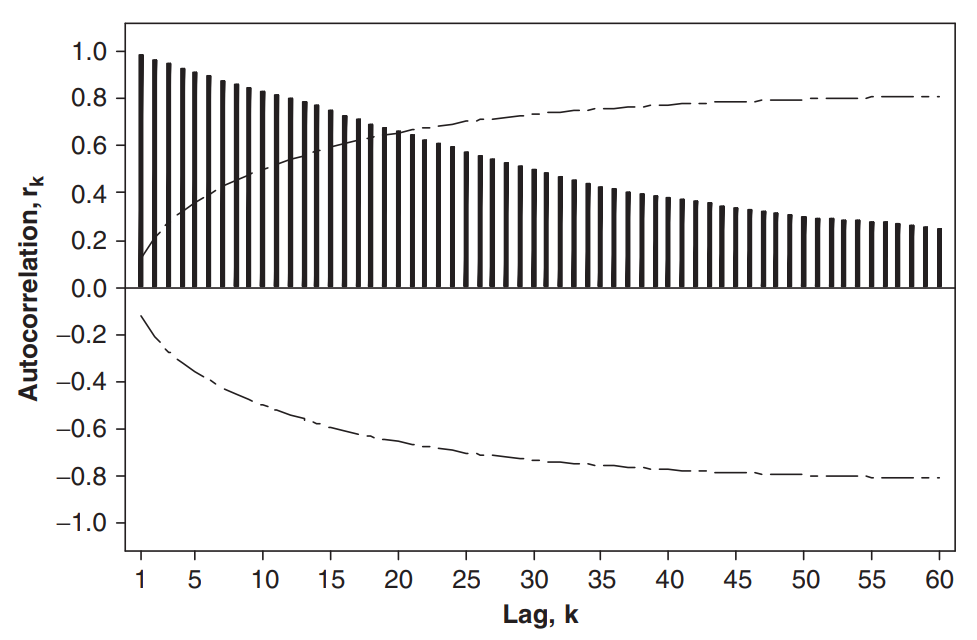
즉 몇 개의 시차(lag) 후에도 급격히 감소하거나 $ 0 $ 에 수렴하지 않으며 긴 지연 후에도 여전히 큰 값을 유지한다. 즉 표본 ACF가 매우 천천히 감소(very slowly decays)하고 장기적 지연에서도 여전히 높은 자기상관값을 보이는 지속적인(persistent) 패턴을 가진다. 일반적으로 표본 ACF가 감소하는 것을 확인하는 장기적 기준으로 잡는 $ k $ 는 $ 15 $~$20$ 이다.
'Statistics > Time Series Analysis' 카테고리의 다른 글
정상성 (Stationarity)
장성성(stationarity)을 가진 시계열, 즉 정상시계열(stationary time series) 데이터는 확인하는 시점이 바뀌어도 그 자료의 특징이 변하지 않는 시계열이다. 특히 엄격한 정상성(strict stationarity)을 가정하면 그 성질이 시간의 원점 변화에 영향을 받지 않아 관측값 $ y_t, y_{t+1}, \cdots, y_{t+n} $ 의 결합확률분포(joint probability distribution)가 $ y_{t+k}, y_{t+k+1}, \cdots, y_{t+k+n} $ 과 완전히 동일(exactly same)하다. 이러한 정상성 가저은 $ n = 0 $ 일 때 $ y_t $ 의 확률분포가 모든 시간(time periods)에 대해 동일하다는 것을 의미하며 이를 $ f(y) $ 로 표현 가능하다.
정상시계열은 그래프로 그렸을 때 일정한 수준을 중심으로 변동하는 경향을 보인다. 당연하게도 확률분포가 원점 변화에 영향을 받지 않기 때문이다. 예를 들어 아래와 같은 의약품 판매 데이터는 정상시계열로 볼 수 있다.

반대로 원점에 따라 변화하는, 예를 들어 아래와 같이 증가하는 시계열은 비정상시계열(non-stationary time series)이라 한다.

정상성은 일종의 통계적 평형(statistical equilibrium) 또는 안정성(stability)을 의미한다. 즉 정상시계열은 다음과 같은 일정한 평균과 분산을 가진다.
$$ \mu_y = E(y) = \int_{-\infty}^{\infty} y f(y) dy $$
$$ \sigma^2_y = \mathrm{Var}(y) = \int_{-\infty}^\infty (y - \mu_y)^2 f(y) dy $$
이러한 평균과 분산은 표본 데이터를 사용하여 추정하는 것이 일반적이다. 표본평균과 표본분산은 아래와 같다.
$$ \bar{y} = \hat{\mu}_y = \frac{1}{T} \sum_{i=1}^T y_t $$
$$ S^2 = \hat{\sigma}^2_y = \frac{1}{T} \sum_{t=1}^T (y_t - \bar{y})^2 $$
이때 특이하게도 일반적인 표본분산과 다르게 $ 1/(T-1) $ 이 아니라 $ 1/T $ 를 사용한다. 시계열 분석에서 흔히 사용되는 방식으로 보통 $ T $ 가 크기에 $ T-1 $ 과 차이가 크지 않다.
자기공분산 및 자기공분산 함수 (Autocovariance and Autocovariance Function)
만약 시계열이 정상시계열이라면 이는 특정 간격 $ k $ 만큼 떨어진 두 개의 관측값, 즉 $ y_t $ 와 $ y_{t+k} $ 의 결합확률분포가 모든 시간 $ t $ 에 대해 동일하다는 것을 의미하고 이러한 결합확률분포에 대해 더 알아보기 위해 동일한 간격 $ k $ 만큼 떨어진 데이터 쌍 $(y_t, y_{t+k}) $ 에 대해 산점도(scatter plot)을 그려볼 수 있다. 여기서 $ k $ 를 시차(lag)라 한다.
어떤 그래프는 아래와 같이 무상관(uncorrelated)일 수 있다. 즉 현재 시점의 값이 $k $ 시차 이후의 값, 여기서는 다음 시점의 값을 예측하는 데에 도움이 되지 않는다.

또는 아래와 같이 상관관계가 나타날 수도 있다. 아래와 같이 양의 상관관계가 나타난다는 것은 직전 값이 작다면 그 다음 값도 작고, 직전 값이 크다면 그 다음 값도 크다는 이야기이다. 즉 현재 값이 다음 값에 영향을 미친다.

시계열의 특정 시간 $ t $ 에 대해서 다른 시간 $ t+k $ 에서의 값과의 공분산(covariance)을 시차 $ k $ 에서의 자기공분산(autocovariance at lag $ k $)이라 하고 다음과 같이 정의한다.
$$ \gamma_k = \mathrm{Cov} (y_t, y_{t+k}) = E[(y_t - \mu)(y_{t+k} - \mu)] $$
그리고 이러한 $ \gamma_k $ 값들의 집합을 자기공분산 함수(autocovariance function)라 한다. 특히 $ k = 0 $ 일 때 자기공분산은 $ \gamma_0 = \sigma_y^2 $ 으로 분산과 같다. 그리고 이는 앞서 말했듯이 정상시계열에서 항상 일정하다.
자기상관계수 및 자기상관함수 (Autocorrelation Coefficient and Autocorrelation Function)
자기상관계수는 다음과 같이 정의된다.
$$ \rho_k = \frac{E[y_t-\mu)(y_{t+k}-\mu)]}{\sqrt{E[(y_t-\mu)^2]E[(y_{t+k}-\mu)^2]}} = \frac{\mathrm{Cov}(y_t, y_{t+k})}{\mathrm{Var}(y_t)} = \frac{\gamma_k}{\gamma_0} $$
그리고 이러한 $ \rho_k $ 값들의 집합을 자기상관함수(ACF, autocorrelation function)라 한다. 정의상 $ \rho_0 = 1 $ 이고, 자기상관함수(ACF)는 시계열의 측정 단위(scale of measurement)에 독립적이므로 무차원(dimensionless) 값이다. 더불어 $ \rho_k = \rho_{-k} $ 이다. 즉 $ 0 $ 을 중심으로 대칭적이며 범위가 $ [-1, 1] $ 이라는 특성을 가진다.
약한 정상성 및 엄격한 정상성 (Weak Stationarity and Strict Stationarity)
어떤 시계열이 유한한 평균(finite mean)과 유한한 자기공분산 함수(finite autocovariance function)을 가지면 이를 2차 정상시계열(second-order stationary time series) 혹은 2차 약한 정상시계열(weakly stationary of order 2 time series)이라 한다.
만약 모든 시점에서 관측값들의 결합확률분포(joint probability distribution)가 다변량 정규분포(multivariate normal distribution)를 따른다면 해당 시계열은 엄격한 정상시계열(strictly stationary time series)이라 한다.
추정
유한한 길이를 가진 시계열 데이터 $y_1, y_2, \cdots, y_T $ 에서 자기공분산 및 자기상관함수를 추정하면 일반적으로 아래와 같은 추정값이 사용된다.
$$ c_k = \hat{\gamma}_k = \frac{1}{T} \sum_{t=1}^{T-k} (y_t - \bar{y}) (y_{t+k}-\bar{y}) , \qquad (k =0, 1, 2, \cdots, K) $$
$$ r_k = \hat{\rho}_k = \frac{c_k}{c_0} , \qquad (k = 0, 1, 2, \cdots, K) $$
신뢰할 수 있는 자기상관함수(ACF) 추정을 위해서는 최소 50개 이상의 데이터가 필요하고 최대 지연값 $ K $ 는 보통 $ K \approx T/4 $ 로 계산한다.
특정 시차(lag) $ k $ 에서 자기상관계수 $ \rho_k $ 가 $ 0 $ 인지 확인해야 하는 경우가 있다. 이를 위해 표본 자기상관계수 $ r_k $ 를 표준오차(standard error)와 비교할 수 있다. 만약 무상관(uncorrelated)이라면, 즉 모든 $ k $ 에 대해 $ \rho_k = 0 $ 이 성립한다고 가정하면 표본 자기상관계수의 분산과 표준오차는 아래와 같다.
$$ \mathrm{Var}(r_k) \approx \frac{1}{T} $$
$$ \mathrm{SE}(r_k) \approx \frac{1}{\sqrt{T}} $$
참고로 엄밀히 말하면 정상시계열에 대해서만 자기상관함수(ACF)가 정의되지만, 표본 ACF는 모든 시계열에 대해 계산 가능하다.
이제 $ r_k $ 를 통해 정상성에 대해 확인해보자. 먼저 아래와 같이 시차(lag)에 대한 ACF 값이 나타난다고 해보자.

처음에는 $0.8$ 수준으로 컸지만, 일정 수준 이후 $ 0 $ 을 중심으로 사인파(sinusoidal) 패턴이 나타난다. 이러한 ACF 패턴은 정상시계열의 전형적인 특징이다. 이에 반해 일정한 평균의 무작위 시계열(time series of random values with constant mean)은 아래와 같은 패턴을 보인다.

반대로 비정상시계열은 시차(lag)에 대한 ACF 값이 일반적으로 아래와 같은 패턴을 보인다.

즉 몇 개의 시차(lag) 후에도 급격히 감소하거나 $ 0 $ 에 수렴하지 않으며 긴 지연 후에도 여전히 큰 값을 유지한다. 즉 표본 ACF가 매우 천천히 감소(very slowly decays)하고 장기적 지연에서도 여전히 높은 자기상관값을 보이는 지속적인(persistent) 패턴을 가진다. 일반적으로 표본 ACF가 감소하는 것을 확인하는 장기적 기준으로 잡는 $ k $ 는 $ 15 $~$20$ 이다.