예측 (Forecast)
미래의 어떤 사건 혹은 여러 사건에 대한 추측(prediction)을 말한다. 당연히 여러 분야에서 중요한 이슈이다. 내일의 날씨, 내일의 경제 상황, 내일 환자의 상태 등 다양한 것을 예측해야할 필요가 있다.
간단하게 구분다면 수일에서 수개월 정도의 단기(short-term), 1~2년 정도의 중기(medium-term), 그 이상의 장기(long-term)으로 나눌 수 있다.
그러나 이러한 예측은 쉽지 않다. 어떤 변수가 어떻게 작용하는지도 파악해야 하고, 어느 정도 작용하는지도 파악해야 하며, 예측하고자 하는 시점에 해당 변수들이 어떻게 달라질지도 예측해야 한다. 예를 들어서 1966년 월스트리트저널은 세기가 바뀔 즈음 미국 컴퓨터는 22만대 가량에 이를 것이라 예측했지만, 당연히 훨씬 많은 수의 컴퓨터가 미국에 보급되었다.
시계열 분석 (Time Series Analysis)
시계열은 말 그대로 관심 변수에 대한 시간 지향적(time-oriented) 혹은 연대기적 관찰 시퀀스(chronological sequence of observations)이다. 시계열 분석에서 예측은 시계열 데이터를 파악하고 그를 통해 미래를 추정하는 것이다. 참고로 예측해야 하는 기간, 즉 몇 개의 미래 시점까지 예측할 것인지가 예측 기간(forecast horizon)이고, 새로운 예측값을 얼마나 자주 생성하는지에 대한 것, 즉 예측 업데이트 주기가 예측 주기(forecast interval)이다.
이러한 예측은 크게 두 가지로 나눌 수 있다. 하나는 정성적 방법론(qualitative forecasting techniques)이고, 다른 하나는 정량적 방법론(quantitative forecasting techniques)이다. 정성적 방법론은 이름대로 주관적 판단에 크게 의존한다. 과거 사례나 유사한 제품 혹은 서비스 이력이 거의 없거나 없을 때 해당 분야의 전문가에 의존하여 판단하는 것이 일반적이다.
정량적 방법론은 예측 모델을 공식적으로 활용한다. 이 모델은 데이터 패턴을 요약하고, 변수의 과거 값과 현재 값 사이의 통계적 관계(statistical relationship)를 나타낸다. 그리고 가장 중요하게 이 모델을 사용하여 데이터 패턴을 미래로 투영, 즉 예측하게 된다. 흔히 사용되는 모델은 회귀분석(regression), 스무딩(smoothing), 일반 시계열 모형(general time series models) 정도이다.
간단하게 소개하자면 회귀분석은 원인적 예측 모델(causal forecasting models)로 관심 변수와 예측 변수 간의 관계를 활용한다. 스무딩은 이전 관측값들에 간단한 함수를 사용하여 관심 변수에 대한 예측값을 제공하는 방법이다. 쉽게 사용 가능하며 만족스러운 결과를 얻을 수 있다는 점에서 경험적(heuristically)으로 사용된다. 일반 시계열 모형은 과거 데이터의 통계적 특성을 통해 공식적 모델을 설정한 후 모델의 미지 파라미터를 추정하는 방법으로 일반적으로 최소제곱법(least squares)을 활용한다.
시계열 데이터 특징
시계열 데이터를 그래프로 표현하면 무작위성(random), 추세(trends), 수준 이동(level shifts), 주기성(periods 또는 cycles), 이상치(unusual observations), 또는 이러한 패턴들의 복합적인 형태(combination of patterns)를 보인다. 참고로 시계열 데이터에서 정상성(stationary)이란 쉽게 말하면 평균과 분산이 일정한 것을 말한다. 만약 만족하지 못하면 비정상성(non-stationary)이라 한다.
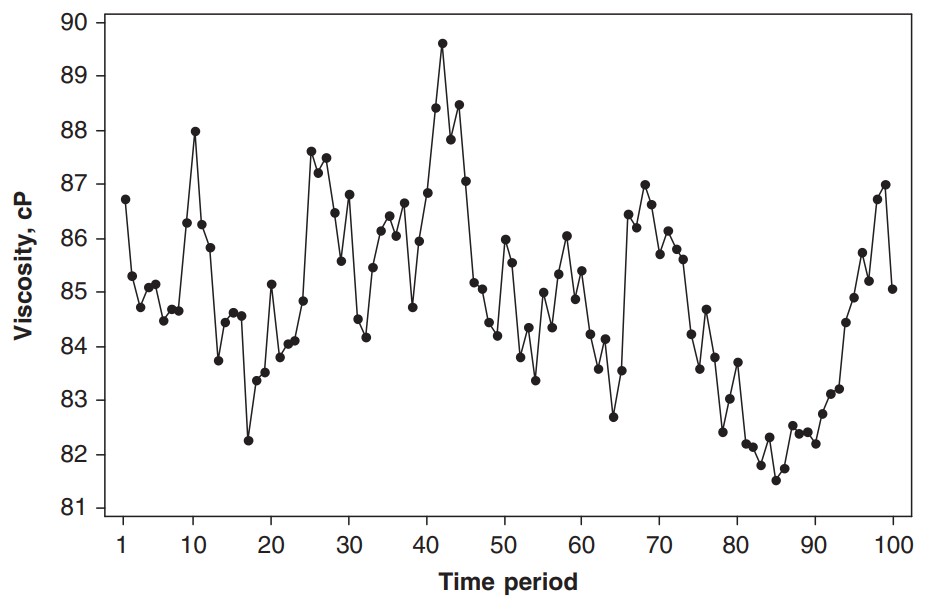
화학 제조 공정과 같은 연속적 프로세스에서는 결과 값들이 종종 양의 자기상관(positive autocorrelation)을 나타낸다. 즉 장기 평균보다 높은 값 뒤에는 계속 높은 값이 나타나는 경향이 있고, 평균보다 낮은 값 뒤에는 계속 낮은 값이 나타나는 경향이 있다.
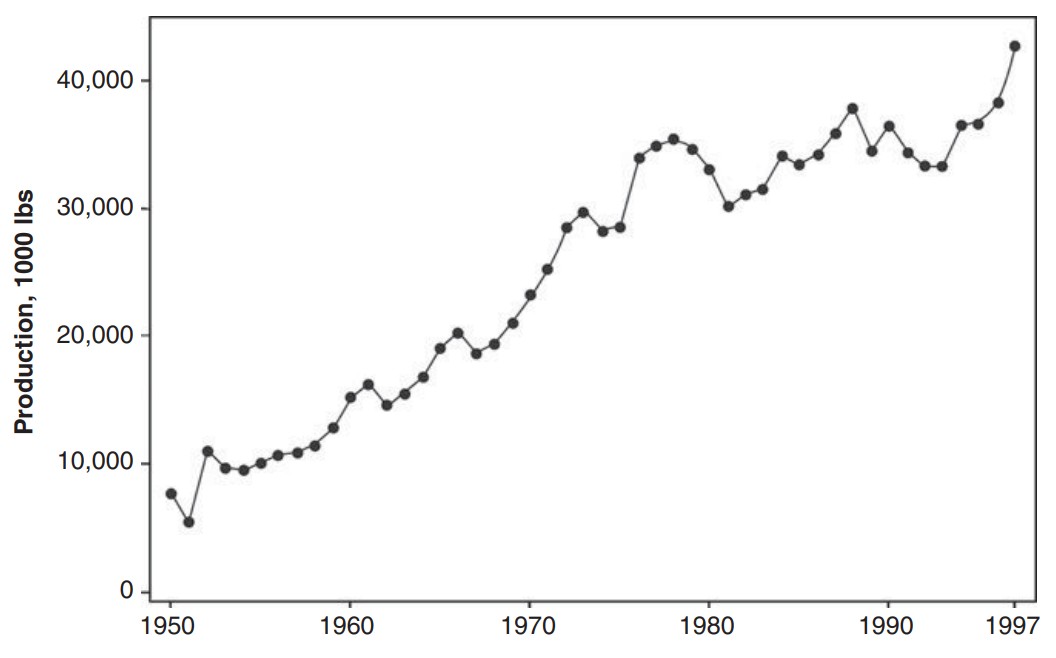
또 선형적 추세(linear trend)가 아래와 같이 나타나기도 한다. 위 화학 제조 공정과 같은 시계열 자료에서는 장기 평균이 의미가 있지만, 아래 블루 및 고르곤졸라 치즈 미국 연간 생산량 자료와 같이 장기 추세가 존재하는 자료에서는 장기 평균이 의미가 없을 수 있다.
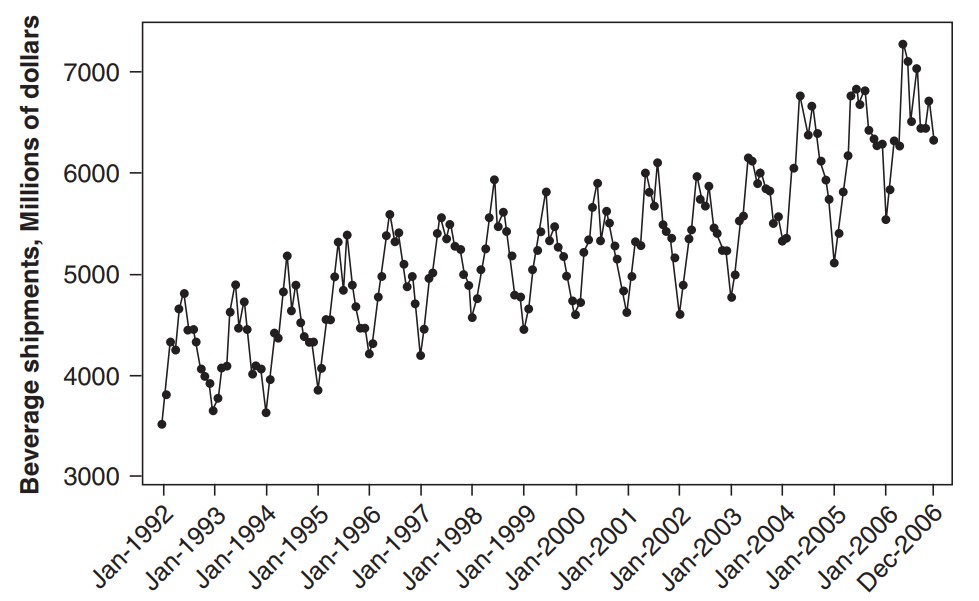
또는 주기적 패턴(cyclic pattern)이 시계열 그래프에 나타날 수도 있다. 아래는 미국 음료 제조사의 월별 출하량 그래프인데, 각 연도 내에서 패턴이 발견된다.
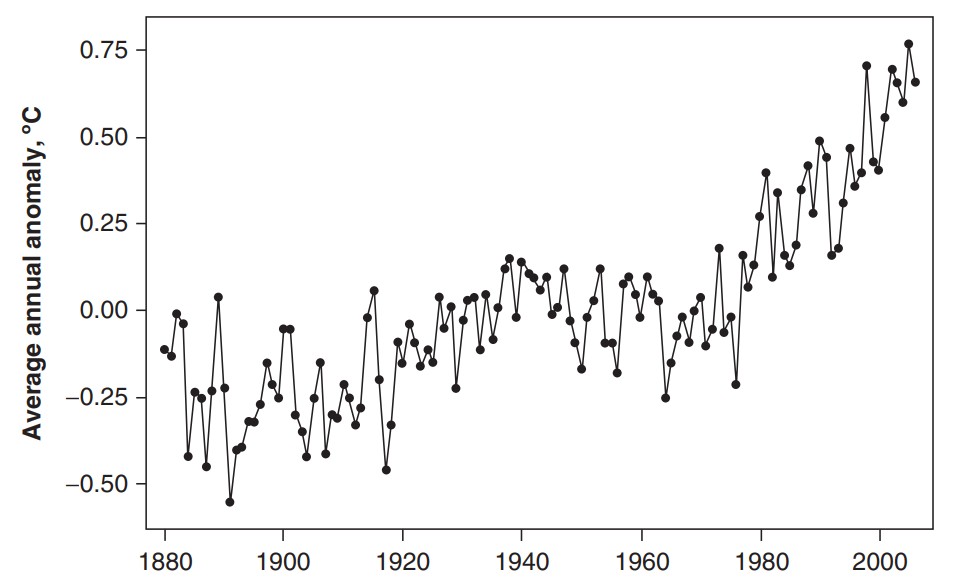
또 기존의 패턴을 깰 수도 있다. 아래 그래프는 지구 온난화(global warming)와 관련하여 연간 평균 온도를 나타낸 것이다. 1960년대 즈음까지 일정 수준을넘어가지 않지만, 1970년 즈음 특정 패턴을 깨고 상승하는 것으로 보인다.
주가 및 금리와 같은 비즈니스 데이터에서는 흔히 비정상성(non-stationary)을 보인다. 즉 시계열 데이터가 일정한 평균을 가지지 않는다.
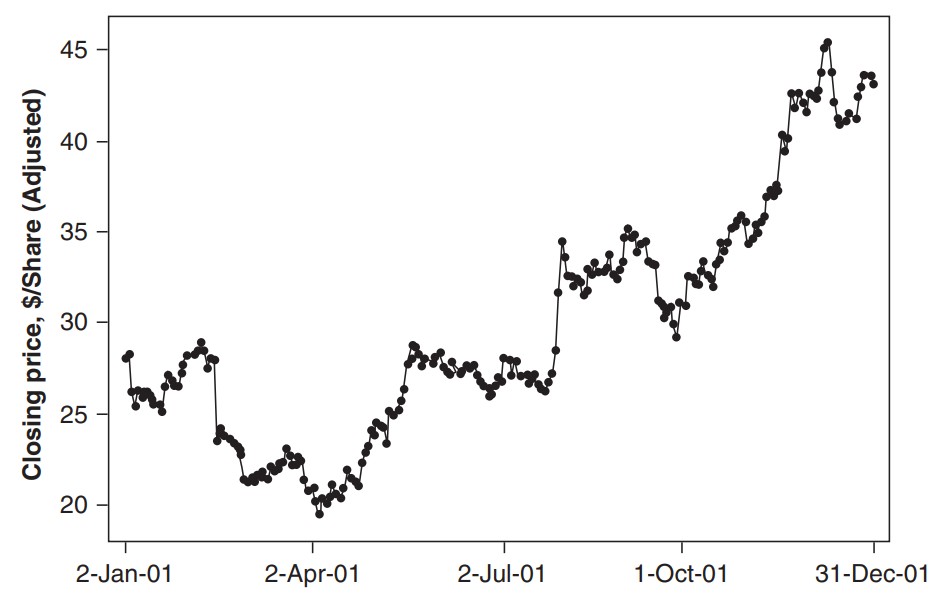
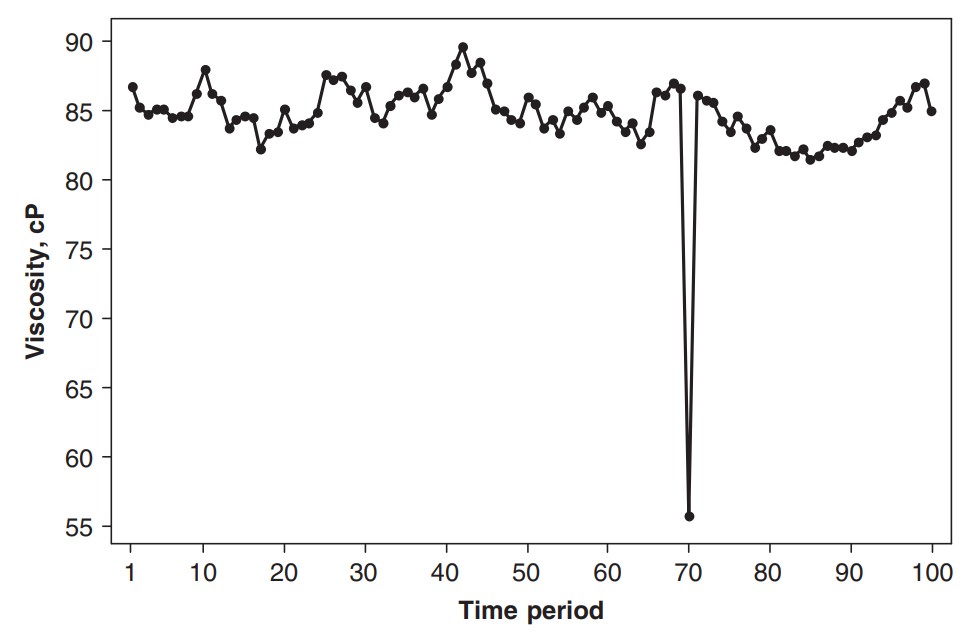
이런 데이터에서는 여느 데이터와 마찬가지로 이상치(outlier)가 존재할 수도 있다. 아래는 제약 제품 매출 그래프인데 85 정도라 예상되는 값에 55가 들어가 있다. 사람의 실수, 혹은 수집 시스템 오류로 노이즈(noise)가 있을 수 있다.
예측 프로세스 (Forecasting Process)
예측을 위해서는 다음과 같은 프로세스를 거쳐야 한다.

먼저 문제 정의(problem definition) 부분은 말 그대로 문제를 정의하는 부분이다. 이때 예측 기간(forecast horizon)과 예측 주기(forecast interval)을 설정하고, 어느 수준의 예측 정확도(forecast accuracy)가 필요한지 확인해야 한다. 예측 모델이 성공적으로 사용되기 위한 대부분 조건은 이 단계에서 결정된다.
데이터 수집(data collection) 단계에서는 말 그대로 예측하려는 변수와 관련된(relevant) 과거 데이터를 확보한다.
데이터 분석(data analysis) 단계는 사용할 예측 모델 선택을 위한 중요한 사전 단계이다. 앞서 시계열 데이터의 특성으로 보였던 추세(trend), 계절성(seasonality) 혹은 주기(cycle) 등을 확인하고, 데이터의 수치적 요약을 통해 그 특성을 파악한다. 이를 보통 탐색적 데이터 분석(EDA, exploratory data analysis)라 하기도 한다. 중요한 것은 데이터의 특성에 대한 감(feel)을 잡는 것이다. 이 단계에서 데이터 정제(data cleaning)을 진행하기도 한다. 결측값(missng data), 이상치(outlier) 등 비정상적인 값(unusual values)이 존재하는지 확인하고 이를 처리한다. 결측값을 대치(imputation)할 때는 평균값 혹은 중앙값 혹은 최빈값을 사용하거나 확률적 평균값(stochastic mean value) 혹은 회귀(regression) 등을 활용한다.
모델 선택 및 피팅(model selection and fitting) 단계에서는 앞선 단계들을 통해 모델을 선택하고, 모델의 미지 파라미터를 추정(estimating)하는, 즉 피팅을 하는 단계이다. 모델의 적합성(quality of model fit)을 평가하고, 기본 가정(assumptions)이 만족하는지 점검한다.
모델에 대한 피팅이 끝났다면 모델 검증(model validation) 단계로 넘어가 모델이 실제 적용 상황에서 얼마나 잘 작동할지 파악한다. 이때 과거 데이터를 얼마나 잘 맞추는지에 대한 평가 이상의 평가가 요구된다. 즉 과적합(overfitting)을 방지해야 한다. 이를 위해 데이터를 분할(data splitting)하고, 일반화 가능성(generalizability)을 기준으로 평가한다.
모델 검증이 끝나면 이 예측 모델을 배포(forecasting model deployment)한다. 이 단계에서는 모델 활용 방법, 데이터 소스 및 기타 필수 정보를 사용자에게 안정적으로 제공되도록 해야 한다.
예측 모델 성능 모니터링(monitoring forecasting model performance)을 통해 모델 배포 후에도 모델이 정상적이고 지속적으로 원하는 동작을 수행하는지 확인한다.
'Statistics > Time Series Analysis' 카테고리의 다른 글
예측 (Forecast)
미래의 어떤 사건 혹은 여러 사건에 대한 추측(prediction)을 말한다. 당연히 여러 분야에서 중요한 이슈이다. 내일의 날씨, 내일의 경제 상황, 내일 환자의 상태 등 다양한 것을 예측해야할 필요가 있다.
간단하게 구분다면 수일에서 수개월 정도의 단기(short-term), 1~2년 정도의 중기(medium-term), 그 이상의 장기(long-term)으로 나눌 수 있다.
그러나 이러한 예측은 쉽지 않다. 어떤 변수가 어떻게 작용하는지도 파악해야 하고, 어느 정도 작용하는지도 파악해야 하며, 예측하고자 하는 시점에 해당 변수들이 어떻게 달라질지도 예측해야 한다. 예를 들어서 1966년 월스트리트저널은 세기가 바뀔 즈음 미국 컴퓨터는 22만대 가량에 이를 것이라 예측했지만, 당연히 훨씬 많은 수의 컴퓨터가 미국에 보급되었다.
시계열 분석 (Time Series Analysis)
시계열은 말 그대로 관심 변수에 대한 시간 지향적(time-oriented) 혹은 연대기적 관찰 시퀀스(chronological sequence of observations)이다. 시계열 분석에서 예측은 시계열 데이터를 파악하고 그를 통해 미래를 추정하는 것이다. 참고로 예측해야 하는 기간, 즉 몇 개의 미래 시점까지 예측할 것인지가 예측 기간(forecast horizon)이고, 새로운 예측값을 얼마나 자주 생성하는지에 대한 것, 즉 예측 업데이트 주기가 예측 주기(forecast interval)이다.
이러한 예측은 크게 두 가지로 나눌 수 있다. 하나는 정성적 방법론(qualitative forecasting techniques)이고, 다른 하나는 정량적 방법론(quantitative forecasting techniques)이다. 정성적 방법론은 이름대로 주관적 판단에 크게 의존한다. 과거 사례나 유사한 제품 혹은 서비스 이력이 거의 없거나 없을 때 해당 분야의 전문가에 의존하여 판단하는 것이 일반적이다.
정량적 방법론은 예측 모델을 공식적으로 활용한다. 이 모델은 데이터 패턴을 요약하고, 변수의 과거 값과 현재 값 사이의 통계적 관계(statistical relationship)를 나타낸다. 그리고 가장 중요하게 이 모델을 사용하여 데이터 패턴을 미래로 투영, 즉 예측하게 된다. 흔히 사용되는 모델은 회귀분석(regression), 스무딩(smoothing), 일반 시계열 모형(general time series models) 정도이다.
간단하게 소개하자면 회귀분석은 원인적 예측 모델(causal forecasting models)로 관심 변수와 예측 변수 간의 관계를 활용한다. 스무딩은 이전 관측값들에 간단한 함수를 사용하여 관심 변수에 대한 예측값을 제공하는 방법이다. 쉽게 사용 가능하며 만족스러운 결과를 얻을 수 있다는 점에서 경험적(heuristically)으로 사용된다. 일반 시계열 모형은 과거 데이터의 통계적 특성을 통해 공식적 모델을 설정한 후 모델의 미지 파라미터를 추정하는 방법으로 일반적으로 최소제곱법(least squares)을 활용한다.
시계열 데이터 특징
시계열 데이터를 그래프로 표현하면 무작위성(random), 추세(trends), 수준 이동(level shifts), 주기성(periods 또는 cycles), 이상치(unusual observations), 또는 이러한 패턴들의 복합적인 형태(combination of patterns)를 보인다. 참고로 시계열 데이터에서 정상성(stationary)이란 쉽게 말하면 평균과 분산이 일정한 것을 말한다. 만약 만족하지 못하면 비정상성(non-stationary)이라 한다.
화학 제조 공정과 같은 연속적 프로세스에서는 결과 값들이 종종 양의 자기상관(positive autocorrelation)을 나타낸다. 즉 장기 평균보다 높은 값 뒤에는 계속 높은 값이 나타나는 경향이 있고, 평균보다 낮은 값 뒤에는 계속 낮은 값이 나타나는 경향이 있다.

또 선형적 추세(linear trend)가 아래와 같이 나타나기도 한다. 위 화학 제조 공정과 같은 시계열 자료에서는 장기 평균이 의미가 있지만, 아래 블루 및 고르곤졸라 치즈 미국 연간 생산량 자료와 같이 장기 추세가 존재하는 자료에서는 장기 평균이 의미가 없을 수 있다.

또는 주기적 패턴(cyclic pattern)이 시계열 그래프에 나타날 수도 있다. 아래는 미국 음료 제조사의 월별 출하량 그래프인데, 각 연도 내에서 패턴이 발견된다.

또 기존의 패턴을 깰 수도 있다. 아래 그래프는 지구 온난화(global warming)와 관련하여 연간 평균 온도를 나타낸 것이다. 1960년대 즈음까지 일정 수준을넘어가지 않지만, 1970년 즈음 특정 패턴을 깨고 상승하는 것으로 보인다.

주가 및 금리와 같은 비즈니스 데이터에서는 흔히 비정상성(non-stationary)을 보인다. 즉 시계열 데이터가 일정한 평균을 가지지 않는다.

이런 데이터에서는 여느 데이터와 마찬가지로 이상치(outlier)가 존재할 수도 있다. 아래는 제약 제품 매출 그래프인데 85 정도라 예상되는 값에 55가 들어가 있다. 사람의 실수, 혹은 수집 시스템 오류로 노이즈(noise)가 있을 수 있다.

예측 프로세스 (Forecasting Process)
예측을 위해서는 다음과 같은 프로세스를 거쳐야 한다.

먼저 문제 정의(problem definition) 부분은 말 그대로 문제를 정의하는 부분이다. 이때 예측 기간(forecast horizon)과 예측 주기(forecast interval)을 설정하고, 어느 수준의 예측 정확도(forecast accuracy)가 필요한지 확인해야 한다. 예측 모델이 성공적으로 사용되기 위한 대부분 조건은 이 단계에서 결정된다.
데이터 수집(data collection) 단계에서는 말 그대로 예측하려는 변수와 관련된(relevant) 과거 데이터를 확보한다.
데이터 분석(data analysis) 단계는 사용할 예측 모델 선택을 위한 중요한 사전 단계이다. 앞서 시계열 데이터의 특성으로 보였던 추세(trend), 계절성(seasonality) 혹은 주기(cycle) 등을 확인하고, 데이터의 수치적 요약을 통해 그 특성을 파악한다. 이를 보통 탐색적 데이터 분석(EDA, exploratory data analysis)라 하기도 한다. 중요한 것은 데이터의 특성에 대한 감(feel)을 잡는 것이다. 이 단계에서 데이터 정제(data cleaning)을 진행하기도 한다. 결측값(missng data), 이상치(outlier) 등 비정상적인 값(unusual values)이 존재하는지 확인하고 이를 처리한다. 결측값을 대치(imputation)할 때는 평균값 혹은 중앙값 혹은 최빈값을 사용하거나 확률적 평균값(stochastic mean value) 혹은 회귀(regression) 등을 활용한다.
모델 선택 및 피팅(model selection and fitting) 단계에서는 앞선 단계들을 통해 모델을 선택하고, 모델의 미지 파라미터를 추정(estimating)하는, 즉 피팅을 하는 단계이다. 모델의 적합성(quality of model fit)을 평가하고, 기본 가정(assumptions)이 만족하는지 점검한다.
모델에 대한 피팅이 끝났다면 모델 검증(model validation) 단계로 넘어가 모델이 실제 적용 상황에서 얼마나 잘 작동할지 파악한다. 이때 과거 데이터를 얼마나 잘 맞추는지에 대한 평가 이상의 평가가 요구된다. 즉 과적합(overfitting)을 방지해야 한다. 이를 위해 데이터를 분할(data splitting)하고, 일반화 가능성(generalizability)을 기준으로 평가한다.
모델 검증이 끝나면 이 예측 모델을 배포(forecasting model deployment)한다. 이 단계에서는 모델 활용 방법, 데이터 소스 및 기타 필수 정보를 사용자에게 안정적으로 제공되도록 해야 한다.
예측 모델 성능 모니터링(monitoring forecasting model performance)을 통해 모델 배포 후에도 모델이 정상적이고 지속적으로 원하는 동작을 수행하는지 확인한다.