변이도 (Variogram)
시계열의 정상성(stationarity)을 판단하는 방법으로는 데이터를 시각화하여 충분히 긴 시간동안 같은 평균이나 분산을 유지하는지 확인하거나, 표본 자기상관함수(ACF)를 계산한 후 시각화하는 방법이 있다. 그러나 이러한 방법은 시계열의 길이가 제한되어 있거나, 추세(trend)나 계절성(seasonality) 등의 문제로 실제 상황에서 사용하기란 쉽지 않다.
이때 변이도(variogram)을 이용할 수 있다. 변이도는 관측값들의 시공간적 연관성(correlation)을 표현하는 함수로 다음과 같이 정의된다.
$$ G_k = \frac{\mathrm{Var}(y_{t+k}-y_t)}{\mathrm{Var}(y_{t+1}-y_t)}, \qquad (k = 1, 2, \cdots) $$
즉 $ k $ 의 시차(lag)를 둔 관측값 차이에 대한 분산을 $ 1 $ 의 시차를 둔 관측값의 차이 분산과 비교한 상대적 크기로 나타낸다. 또한 만약 정상시계열(stationary time series)이라면 다음과 같다.
$$ G_k = \frac{1 - \rho_k}{1- \rho_1} $$
분산의 정의를 활용해 $ \mathrm{Var}(y_{t+k} - y_t) $ 를 전개하면 다음과 같다.
$ \mathrm{Var}(y_{t+k} - y_t) = \mathrm{Var}(y_{t+k}) + \mathrm{Var}(y_t) - 2 \mathrm{Cov}(y_{t+k}, y_t) $
이제 정상성을 가정하자. 그렇다면 시계열의 분산은 시간 $ t $ 에 무관하므로 다음과 같다.
$ \mathrm{Var}(y_t) = \gamma_0 $
$ \mathrm{Cov}(y_{t+k}, y_t) = \gamma_k $
그러므로 $ \mathrm{Var}(y_{t+k} - y_t) $ 는 다음과 같다.
$ \mathrm{Var}(y_{t+k} - y_t) = \gamma_0 + \gamma_0 - 2\gamma_k = 2(\gamma_0 - \gamma_k) $
그렇다면 주어진 식 $ G_k $ 는 다음과 같다.
$ G_k = \dfrac{\mathrm{Var}(y_{t+k}-y_t)}{\mathrm{Var}(y_{t+1}-y_t)} $
$ = \dfrac{2(\gamma_0 - \gamma_k)}{2(\gamma_0 - \gamma_1)} $
$ = \dfrac{\gamma_0 - \gamma_k}{\gamma_0 - \gamma_1} $
여기서 자기상관함수 $ \rho_k $ 의 정의는 다음과 같다.
$ \rho_k = \dfrac{\gamma_k}{\gamma_0} \Leftrightarrow \gamma_k = \gamma_0 \rho_k $
이를 활용하여 $ G_k $ 를 나타내면 다음과 같다.
$ G_k = \dfrac{\gamma_0 - \gamma_0 \rho_k}{\gamma_0 - \gamma_0 \rho_1} $
$ = \dfrac{\gamma_0(1 - \rho_k)}{\gamma_0(1 - \rho_1)} $
이때 $ \gamma_0 \neq 0 $ 이므로 소거 가능하고 따라서 다음과 같다.
$ G_k = \dfrac{1 - \rho_k}{1- \rho_1} $
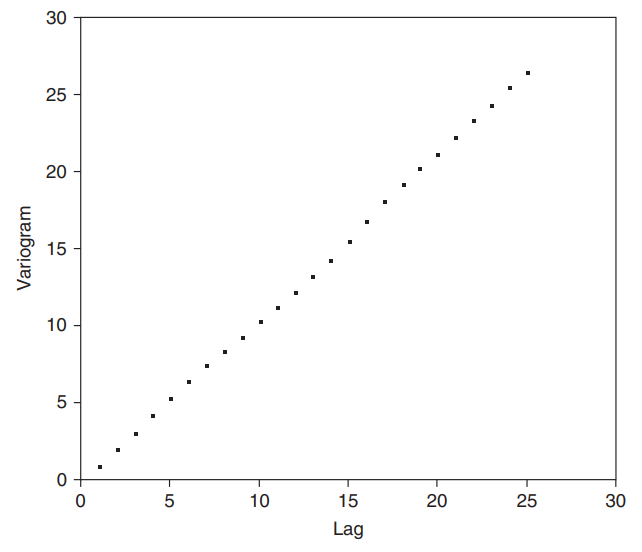
그런데 정상시계열에서 $ \underset{n \to \infty}{\lim} \rho_k = 0 $ 이므로 시차(lag) $ k $ 에 대해 그린다면 $ \dfrac{1}{1 - \rho_1} $ 이라는 점근선(asymptote)에 도달한다. 반면 비정상시계열(non-stationary time series)이라면 $ G_k $ 는 단조증가(monotonically increasing)하게 된다.
추정
변이도(variogram)를 추정하기 위해서 보통 표본분산의 차이들 이용하되, 시차(lag)가 달라짐에 따라 사용 가능한 표본 크기가 달라진다는 점에 유의하면 된다. 우선 다음과 같이 표본분산의 차이 및 표본분산의 차이의 기댓값을 정의하자.
$$ d_t^k = y_{t+k} - y_t, \qquad \bar{d}^k = \frac{1}{T-k} \sum_{t=1}^{T-k} d_t^k $$
그렇다면 $ \mathrm{Var}(y_{t+k}-y_t) $ 에 대한 추정값 $ s_k^2 $ 는 다음과 같다.
$$ s_k^2 = \frac{\sum_{t=1}^{T-k} (d_t^k - \bar{d}^k)^2}{T-k-1} $$
따라서 표본 변이도(sample variogram)은 다음과 같이 정의된다.
$$ \hat{G}_k = \frac{s_k^2}{s_1^2}, \qquad (k = 1, 2, \cdots) $$
즉 먼저 여러 개의 시차(lag)에 대해 연속된 관측값 간 차이를 계산하고, 계산된 차이들의 표본분산을 구한다. 이렇게 얻어진 표본분산들을 시차 $ 1 $ 에서의 첫 번째 차이의 표본분산으로 나누어 표본 변이도를 얻는다.
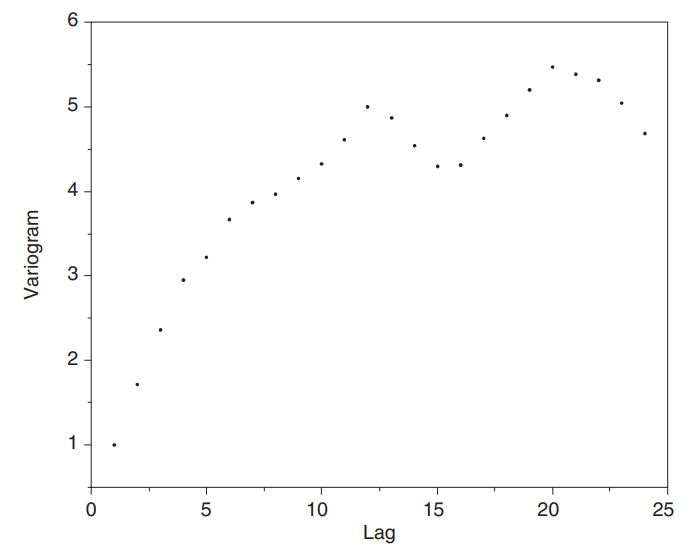
정상시계열에서의 변이도 그래프의 예시는 아래와 같다. 전반적으로 안정적인 수준으로 수렴한 뒤 그 주변에서 약간씩 변동하는 모습을 보여준다.
반면 비정상시계열에서의 변이도 그래프의 예시는 아래와 같다. 고정된 수준(level) 없이 계속 부유(wander)하거나 매우 천천히 감쇠(decay)하는 특징을 보인다.