확률변수 (Random Variable)
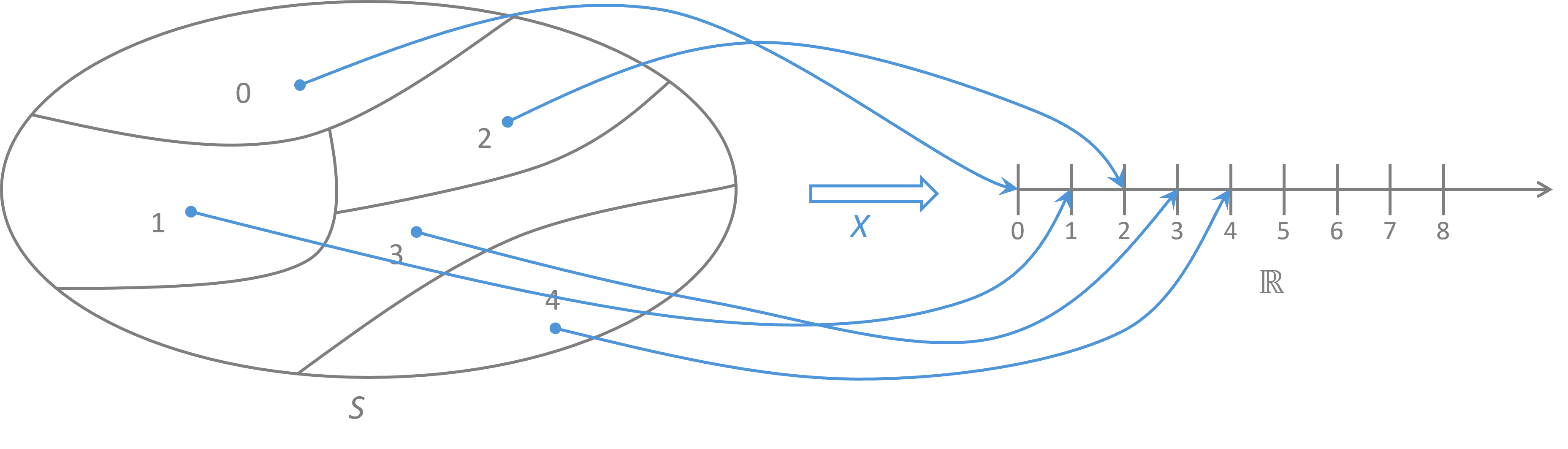
$$ X : S \to \mathbb{R} $$
확률변수란 표본공간을 정의역으로 하고, 실수 값을 치역으로 하는 함수로 확률 실험의 결과를 수치로 나타내는 데에 사용된다. 확률변수의 함수 역시 확률변수이다. 확률 실험의 정보를 어느정도 나타내느냐를 결정하고, 이 확률변수의 분포가 확률분포가 된다.
일반적으로 확률변수 $ X $ 가 가질 수 있는 값의 범위가 셀 수 있는지 없는지에 따라 이산확률변수(discrete random variable)와 연속확률변수(continuous random variable)로 나누지만, 그 외 확률변수도 존재한다. 이산확률변수는 유한개의(finite) 값이나 자연수의 부분집합과 일대일 대응이 가능한(countable) 값으로 구성되어 있는 확률변수이고, 연속확률변수는 셀 수 없는(uncountable) 개수의 실수를 가지는 확률변수이다. 확실하게 구분하기 위해서는 누적분포함수의 개형을 보아야 한다.
변수가 여러 개인 다변량 확률변수의 경우 표본공간에서 $ \mathbb{R} $ 이 아니라 $ \mathbb{R}^n $ 으로 가는 함수로 나타낼 수 있다.
확률분포 (Probability Distribution)
확률변수가 어떤 값을 가질지에 대한 확률을 나타낸다. 명확히 나타내면 다음과 같다.
표본공간 $ S $ 의 사건들의 집합에서 정의된 확률함수를 $ P $ 라고 하면 확률변수 $ X $ 의 분포는 다음과 같은 확률함수 $ P_X() $ 로 정의할 수 있다.
$$ \text{Let } B \subset \mathbb{R}, \quad P_X(B) = P (\{w \in S \mid X(w) \in B\}) $$
이산확률변수의 분포를 이산확률분포, 연속확률변수의 연속확률분포라 한다. 이산확률분포의 경우 확률변수가 가지는 모든 값과 각 값에 대응하는 확률을 표나 공식, 그래프 등을 통해 나타낼 수 있고, 이를 확률질량함수로 표현할 수 있다. 그러나 연속확률변수는 이것이 불가능하기에 확률밀도함수로 표현한다.
이 확률분포에서 지지집합(support)은 확률변수가 가질 수 있는 값들의 집합이다. 특히 이 값에서 확률은 0 이 되지 않는다.
확률질량함수 (Probability Mass Function, PMF)
$$ p_X(x) = P(X=x) $$
$$ \operatorname{supp} p_X : \{ x \in \mathbb{R} \mid p_X(x) > 0 \} $$
이산확률변수에서 특정 값에 대한 확률을 나타내는 함수이다. 즉 함수값이 확률이며, 다음이 성립한다.
- $ 0 \leq p_X(x) \leq 1 $
- $ \sum p_X(x) = 1 $
- $ p_X(a < x \leq b) = \sum_{a < x \leq b} p_X(x) $
누적분포함수 (Cumulative Distribution Function, CDF)
$$ F_X(x) = P(X \leq x) $$
$$ \operatorname{supp} F_X = \{ x \in \mathbb{R} \mid 0 < F_X(x) < 1 \} $$
주어진 확률변수가 특정 값보다 작거나 같은 확률을 나타내는 함수이다. 즉 감소하지 않는(non-decreasing) 함수이다. 확률질량함수와 마찬가지로 함수값이 확률이며, 만약 누적분포함수가 계단 모양(step function)이면 이산확률변수이다. 누적이라는 말을 생략하고 분포함수라고 하기도 하며, 다음이 성립한다.
- $ 0 \leq F_X(x) \leq 1 $
- $ \lim_{x \to - \infty} F_X(x) = 0 $
- $ \lim_{x \to \infty} F_X(x) = 1 $
- $ \lim_{h \to 0^+} F_X(x+h) = F(x) $ | 우측 연속
확률밀도함수 (Probability Density Function, PDF)
$$ f_X(x) = \dfrac{d F_X(x)}{dx}, \quad F_X(x) = \int_{- \infty}^{x} f_X(t) dt $$
$$ \operatorname{supp} f_X = \{ x \in \mathbb{R} \mid f_X(x) > 0 \} $$
연속확률변수의 경우, 한 값으로 실현될 확률은 0 이다. 즉 $ X $ 가 연속확률변수이면 $ P(X=x) = 0, \text{ } \forall x $ 이다. 따라서 연속확률변수의 확률은 $ P(x_1 \leq X \leq x_2) $ 와 같이 구간으로 표현한다. 이때 특정 값에서 확률은 0 이기 때문에 $ \leq $ 와 $ < $ 는 차이가 없다. 즉 $ P(x_1 \leq X \leq x_2) = P(x_1 < X < x_2) = P(x_1 \leq X < x_2) = P(x_1 < X \leq x_2) $ 이다. 누적분포함수로 확인하면 $ P(x_1 \leq X \leq x_2) = F_X(x_2) - F_X(x_1) $ 이다.
연속확률변수는 특정 값에서의 확률이 0 이기 때문에 확률질량함수를 가지지 않고, 이에 대응되는 확률밀도함수를 가진다. 확률밀도함수는 해당 영역의 넓이를 확률로 가지는 함수로 누적분포함수를 미분하여 얻어진다. 다음이 성립하면 확률밀도함수이다.
- $ f_X(x) \geq 0, \quad \forall x $
- $ \int_{- \infty}^{\infty} f_X(x) dx = 1 $
$ f_X $ 가 확률밀도함수라면 미적분학 기본정리에 의해 다음 역시 성립한다.
- $ P(x_1 \leq X \leq x_2) = F_X(x_2) - F_X(x_1) = \int_{x_1}^{x_2} f_X(x) dx $
- $ P(X \leq x) = \int_{- \infty}^{x} f_X(x) dx, \quad P(X \geq x) = \int_{x}^{\infty} f_X(x) dx = 1 - P(X \leq x) $
$ f_X(x) $ 는 $ X = x $ 가 나타날 가능성을 반영하긴 하지만 확률은 아니고, 단지 확률밀도함수의 값일 뿐이다. 확률은 특정 영역의 적분값으로 확인 가능하다.
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [Mathematical Statistics] 확률생성함수(PGF) (0) | 2024.10.09 |
|---|---|
| [Mathematical Statistics] 적률(moment)과 적률생성함수(MGF) (0) | 2024.10.08 |
| [Mathematical Statistics] 확률변수의 기댓값과 분산 (0) | 2024.10.02 |
| [Mathematical Statistics] 전확률의 법칙과 베이즈 정리 (0) | 2024.09.09 |
| [Mathematical Statistics] 확률의 정의와 조건부확률 및 확률법칙 (0) | 2024.09.09 |
확률변수 (Random Variable)

$$ X : S \to \mathbb{R} $$
확률변수란 표본공간을 정의역으로 하고, 실수 값을 치역으로 하는 함수로 확률 실험의 결과를 수치로 나타내는 데에 사용된다. 확률변수의 함수 역시 확률변수이다. 확률 실험의 정보를 어느정도 나타내느냐를 결정하고, 이 확률변수의 분포가 확률분포가 된다.
일반적으로 확률변수 $ X $ 가 가질 수 있는 값의 범위가 셀 수 있는지 없는지에 따라 이산확률변수(discrete random variable)와 연속확률변수(continuous random variable)로 나누지만, 그 외 확률변수도 존재한다. 이산확률변수는 유한개의(finite) 값이나 자연수의 부분집합과 일대일 대응이 가능한(countable) 값으로 구성되어 있는 확률변수이고, 연속확률변수는 셀 수 없는(uncountable) 개수의 실수를 가지는 확률변수이다. 확실하게 구분하기 위해서는 누적분포함수의 개형을 보아야 한다.
변수가 여러 개인 다변량 확률변수의 경우 표본공간에서 $ \mathbb{R} $ 이 아니라 $ \mathbb{R}^n $ 으로 가는 함수로 나타낼 수 있다.
확률분포 (Probability Distribution)
확률변수가 어떤 값을 가질지에 대한 확률을 나타낸다. 명확히 나타내면 다음과 같다.
표본공간 $ S $ 의 사건들의 집합에서 정의된 확률함수를 $ P $ 라고 하면 확률변수 $ X $ 의 분포는 다음과 같은 확률함수 $ P_X() $ 로 정의할 수 있다.
$$ \text{Let } B \subset \mathbb{R}, \quad P_X(B) = P (\{w \in S \mid X(w) \in B\}) $$
이산확률변수의 분포를 이산확률분포, 연속확률변수의 연속확률분포라 한다. 이산확률분포의 경우 확률변수가 가지는 모든 값과 각 값에 대응하는 확률을 표나 공식, 그래프 등을 통해 나타낼 수 있고, 이를 확률질량함수로 표현할 수 있다. 그러나 연속확률변수는 이것이 불가능하기에 확률밀도함수로 표현한다.
이 확률분포에서 지지집합(support)은 확률변수가 가질 수 있는 값들의 집합이다. 특히 이 값에서 확률은 0 이 되지 않는다.
확률질량함수 (Probability Mass Function, PMF)
$$ p_X(x) = P(X=x) $$
$$ \operatorname{supp} p_X : \{ x \in \mathbb{R} \mid p_X(x) > 0 \} $$
이산확률변수에서 특정 값에 대한 확률을 나타내는 함수이다. 즉 함수값이 확률이며, 다음이 성립한다.
- $ 0 \leq p_X(x) \leq 1 $
- $ \sum p_X(x) = 1 $
- $ p_X(a < x \leq b) = \sum_{a < x \leq b} p_X(x) $
누적분포함수 (Cumulative Distribution Function, CDF)
$$ F_X(x) = P(X \leq x) $$
$$ \operatorname{supp} F_X = \{ x \in \mathbb{R} \mid 0 < F_X(x) < 1 \} $$
주어진 확률변수가 특정 값보다 작거나 같은 확률을 나타내는 함수이다. 즉 감소하지 않는(non-decreasing) 함수이다. 확률질량함수와 마찬가지로 함수값이 확률이며, 만약 누적분포함수가 계단 모양(step function)이면 이산확률변수이다. 누적이라는 말을 생략하고 분포함수라고 하기도 하며, 다음이 성립한다.
- $ 0 \leq F_X(x) \leq 1 $
- $ \lim_{x \to - \infty} F_X(x) = 0 $
- $ \lim_{x \to \infty} F_X(x) = 1 $
- $ \lim_{h \to 0^+} F_X(x+h) = F(x) $ | 우측 연속
확률밀도함수 (Probability Density Function, PDF)
$$ f_X(x) = \dfrac{d F_X(x)}{dx}, \quad F_X(x) = \int_{- \infty}^{x} f_X(t) dt $$
$$ \operatorname{supp} f_X = \{ x \in \mathbb{R} \mid f_X(x) > 0 \} $$
연속확률변수의 경우, 한 값으로 실현될 확률은 0 이다. 즉 $ X $ 가 연속확률변수이면 $ P(X=x) = 0, \text{ } \forall x $ 이다. 따라서 연속확률변수의 확률은 $ P(x_1 \leq X \leq x_2) $ 와 같이 구간으로 표현한다. 이때 특정 값에서 확률은 0 이기 때문에 $ \leq $ 와 $ < $ 는 차이가 없다. 즉 $ P(x_1 \leq X \leq x_2) = P(x_1 < X < x_2) = P(x_1 \leq X < x_2) = P(x_1 < X \leq x_2) $ 이다. 누적분포함수로 확인하면 $ P(x_1 \leq X \leq x_2) = F_X(x_2) - F_X(x_1) $ 이다.
연속확률변수는 특정 값에서의 확률이 0 이기 때문에 확률질량함수를 가지지 않고, 이에 대응되는 확률밀도함수를 가진다. 확률밀도함수는 해당 영역의 넓이를 확률로 가지는 함수로 누적분포함수를 미분하여 얻어진다. 다음이 성립하면 확률밀도함수이다.
- $ f_X(x) \geq 0, \quad \forall x $
- $ \int_{- \infty}^{\infty} f_X(x) dx = 1 $
$ f_X $ 가 확률밀도함수라면 미적분학 기본정리에 의해 다음 역시 성립한다.
- $ P(x_1 \leq X \leq x_2) = F_X(x_2) - F_X(x_1) = \int_{x_1}^{x_2} f_X(x) dx $
- $ P(X \leq x) = \int_{- \infty}^{x} f_X(x) dx, \quad P(X \geq x) = \int_{x}^{\infty} f_X(x) dx = 1 - P(X \leq x) $
$ f_X(x) $ 는 $ X = x $ 가 나타날 가능성을 반영하긴 하지만 확률은 아니고, 단지 확률밀도함수의 값일 뿐이다. 확률은 특정 영역의 적분값으로 확인 가능하다.
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [Mathematical Statistics] 확률생성함수(PGF) (0) | 2024.10.09 |
|---|---|
| [Mathematical Statistics] 적률(moment)과 적률생성함수(MGF) (0) | 2024.10.08 |
| [Mathematical Statistics] 확률변수의 기댓값과 분산 (0) | 2024.10.02 |
| [Mathematical Statistics] 전확률의 법칙과 베이즈 정리 (0) | 2024.09.09 |
| [Mathematical Statistics] 확률의 정의와 조건부확률 및 확률법칙 (0) | 2024.09.09 |