분할 (Partition)
표본공간을 상호배타적인 사건들의 합사건으로 표현할 수 있다. 이때 상호배타적인 사건들의 모임을 표본공간의 분할이라 한다. 상호배타적 사건이라는 것은 $ A \cap B = \emptyset $ 을 만족하는 사건을 말한다. 이러한 분할은 아래와 같이 표현할 수 있다.
$$ \bigcup_{i=1}^{\infty} B_i = B_1 \cup B_2 \cdots = S \quad (\forall {i \neq j} , B_i \cap B_j = \emptyset ) $$
전확률의 법칙 (Law of Total Probability)

$ \{ B_1, B_2, \cdots , B_k \} $ 가 $ S $ 의 분할이고, 모든 $ j $ 에 대하여 $ P(B_j) > 0 $ 이면 다음이 성립한다.
$$ P(A) = \sum^k_{i=1} P(A \mid B_i) P(B_i) $$
베이즈 정리 (Bayes' Rule)
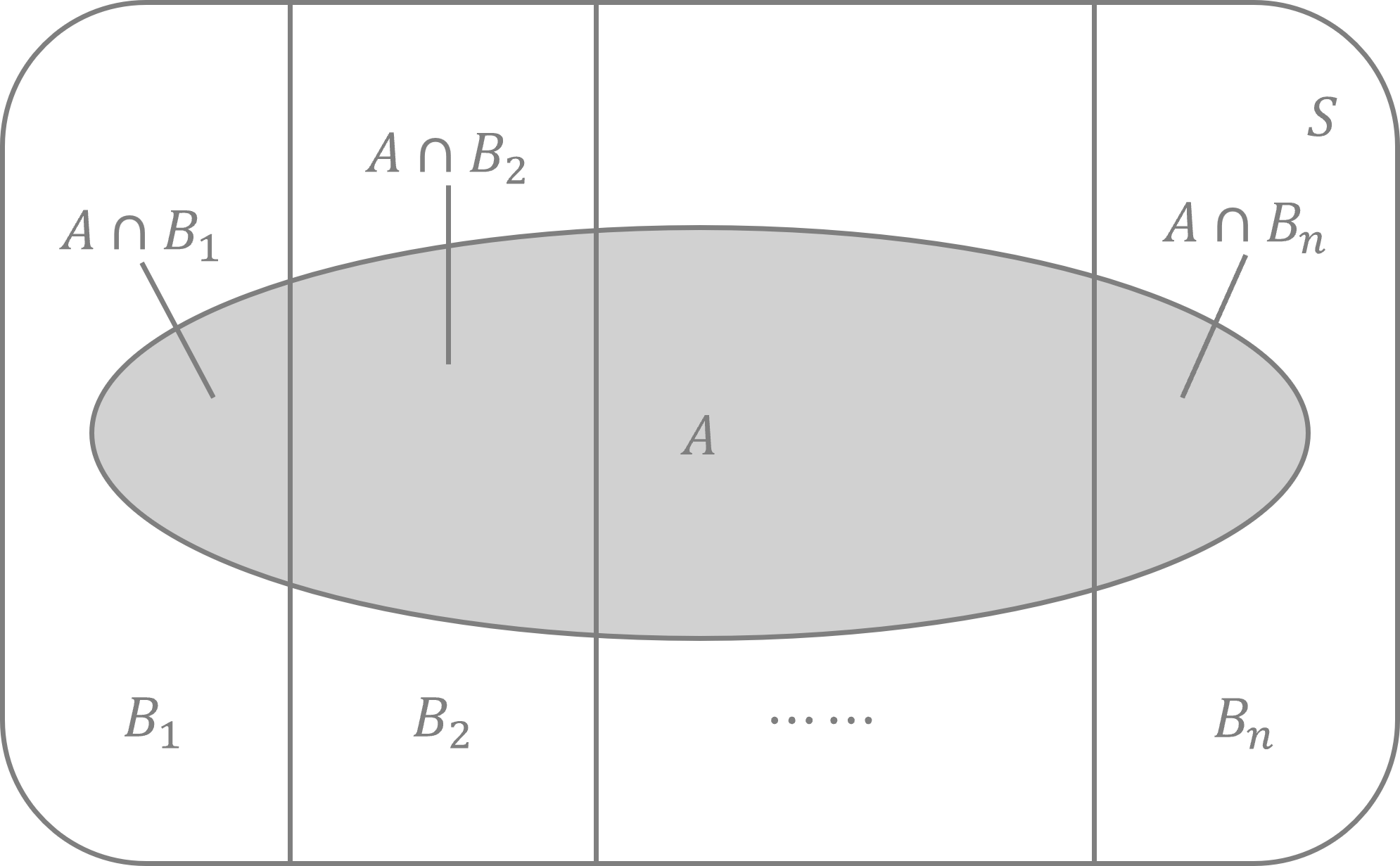
$ \{ B_1, B_2, \cdots , B_k \} $ 가 $ S $ 의 분할이라 가정하자. 이때 다른 사건 $ A $ 에 대하여 $ P(A) \neq 0 $ 이면 전확률의 법칙에 의하여 $ P (B_i \mid A) $ 는 다음과 같이 구할 수 있다.
$$ P(B_i \mid A) = \dfrac{P(B_i \cap A)}{P(A)} = \dfrac{P(A \mid B_i)P(B_i)}{\sum^k_{j=1} P(A \mid B_j)P(B_j)} $$
이때 $ P(B_j) $ 를 사전확률(prior probability), $ P(A \mid B_j) $ 를 우도확률(likelihood probability), $ P(B_j \mid A) $ 를 사후확률(posterior probability)이라 한다.
추가 조건부 (Extra Conditioning)
- 조건부 독립
사건 $ A $ 와 $ B $ 는 주어진 사건 $ E $ 에 대해 조건부 독립이다.
$$ P(A \cap B \mid E) = P(A \mid E)P(B \mid E) $$
- 추가 조건부 전확률의 법칙
$ A_1, \ldots, A_n $ 가 $ S $ 의 분할이고 모든 $ j $ 에 대해 $ P (A_j \cap E ) > 0 $ 이면 다음이 성립한다.
$$ P( B \mid E) = \sum^n_{i=1}P(B \mid A_i, E)P(A_i \mid E) $$
- 추가 조건부 베이즈 정리
$ P(A \cap E) > 0 $ 그리고 $ P(B \cap E) > 0 $ 일 때 다음이 성립한다.
$$ P(A \mid B, E) = \dfrac{P(B \mid A, E)P(A \mid E)}{P(B \mid E)} $$
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [Mathematical Statistics] 확률생성함수(PGF) (0) | 2024.10.09 |
|---|---|
| [Mathematical Statistics] 적률(moment)과 적률생성함수(MGF) (0) | 2024.10.08 |
| [Mathematical Statistics] 확률변수의 기댓값과 분산 (0) | 2024.10.02 |
| [Mathematical Statistics] 확률변수와 확률분포 (0) | 2024.09.25 |
| [Mathematical Statistics] 확률의 정의와 조건부확률 및 확률법칙 (0) | 2024.09.09 |
분할 (Partition)
표본공간을 상호배타적인 사건들의 합사건으로 표현할 수 있다. 이때 상호배타적인 사건들의 모임을 표본공간의 분할이라 한다. 상호배타적 사건이라는 것은 을 만족하는 사건을 말한다. 이러한 분할은 아래와 같이 표현할 수 있다.
전확률의 법칙 (Law of Total Probability)

가 의 분할이고, 모든 에 대하여 이면 다음이 성립한다.
베이즈 정리 (Bayes' Rule)

가 의 분할이라 가정하자. 이때 다른 사건 에 대하여 이면 전확률의 법칙에 의하여 는 다음과 같이 구할 수 있다.
이때 를 사전확률(prior probability), 를 우도확률(likelihood probability), 를 사후확률(posterior probability)이라 한다.
추가 조건부 (Extra Conditioning)
- 조건부 독립
사건 와 는 주어진 사건 에 대해 조건부 독립이다.
- 추가 조건부 전확률의 법칙
가 의 분할이고 모든 에 대해 이면 다음이 성립한다.
- 추가 조건부 베이즈 정리
그리고 일 때 다음이 성립한다.
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [Mathematical Statistics] 확률생성함수(PGF) (0) | 2024.10.09 |
|---|---|
| [Mathematical Statistics] 적률(moment)과 적률생성함수(MGF) (0) | 2024.10.08 |
| [Mathematical Statistics] 확률변수의 기댓값과 분산 (0) | 2024.10.02 |
| [Mathematical Statistics] 확률변수와 확률분포 (0) | 2024.09.25 |
| [Mathematical Statistics] 확률의 정의와 조건부확률 및 확률법칙 (0) | 2024.09.09 |