이진 탐색 트리

탐색작업을 효율적으로 하기 위해 정렬한 이진 트리이다.
루트 노드의 값보다 작은 값은 왼쪽 서브트리에, 큰 값은 오른쪽 서브트리에 있는 것이 특징이다. 이러한 특징 때문에 이진 탐색 트리를 최상위 노드부터 중위순회한다면 오름차순으로 정렬된 값을 얻을 수 있다.
탐색
탐색 연산은 이진 탐색 트리의 정렬을 이용한다. 최상위 노드의 값부터 비교를 시작하는데, 탐색하고자 하는 값과 같다면 탐색 종료, 탐색하고자 하는 값보다 크다면 그보다 더 작은 값을 찾아야 하기 때문에 외쪽 서브트리로 이동, 반대로 탐색하고자 하는 값보다 작다면 그보다 더 큰 값을 찾아야 하기 때문에 오른쪽 서브트리로 이동하여 탐색을 진행한다.
예를 들어 트리에서 5를 탐색한다고 하면 아래와 같이 탐색한다. 탐색 값을 찾으면 해당 노드 포인터를 반환하고, 못 찾으면 NULL을 반환한다.
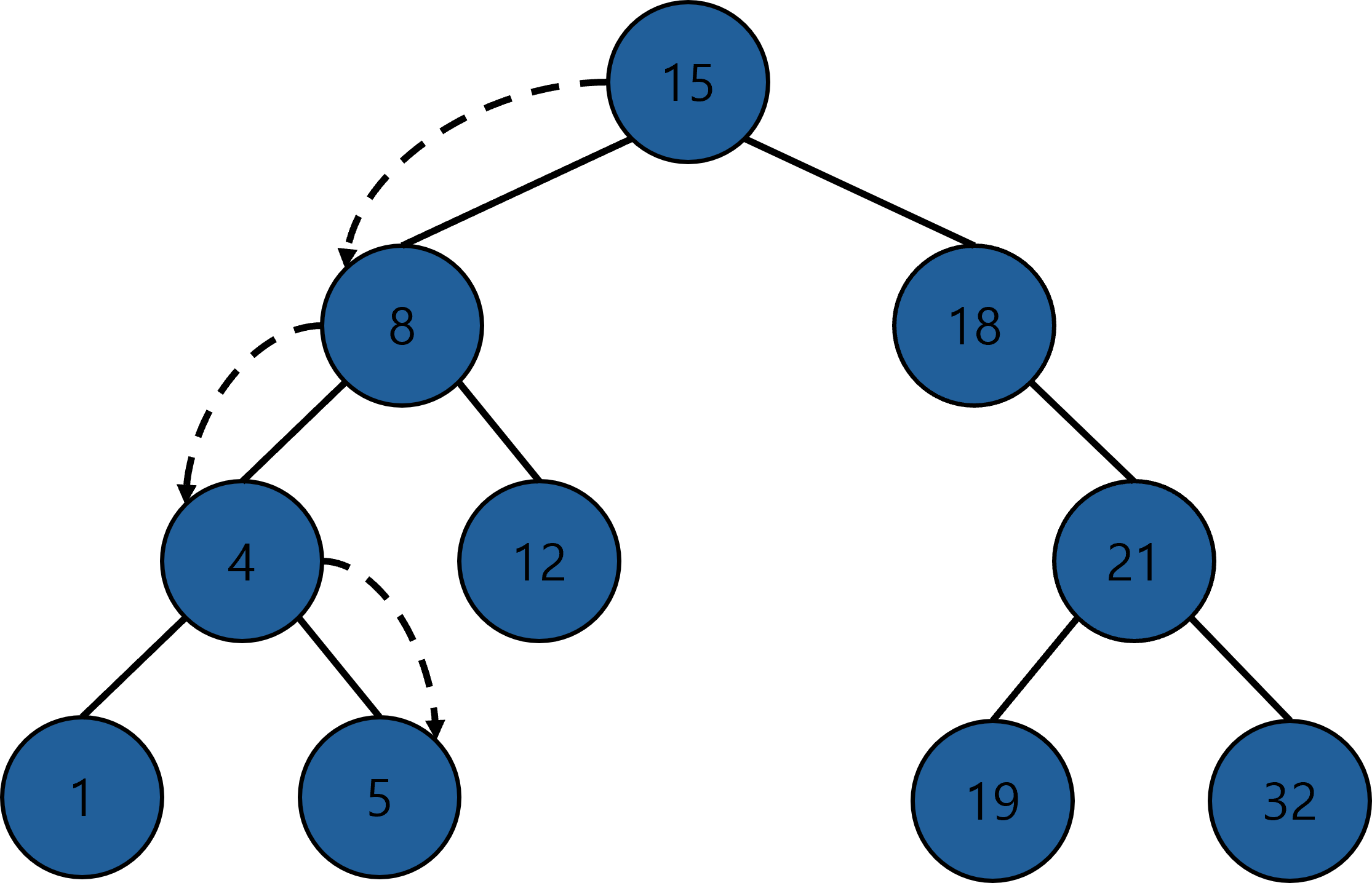
순환적 방법과 반복적 방법으로 구현 가능하다.
다음은 순환적 방법을 구현한 것이다.
TreeNode* search(TreeNode* node, int key)
{
if (node == NULL) {
return NULL;
}
if (key == node->data) {
return node;
} else if (key < node->data) {
return search(node->left, key);
} else {
return search(node->right, key);
}
}반복적 방법은 아래와 같다.
TreeNode* search(TreeNode* node, int key) {
while (node != NULL) {
if (key == node->data) {
return node;
} else if (key < node->data) {
node = node->left;
} else {
node = node->right;
}
}
return NULL;
}반복적 방법이 더 효율적일 가능성이 높다.
삽입
이진 탐색 트리에 원소를 삽입하는 경우 탐색을 통해 먼저 삽입 가능한 위치를 찾아야 한다. 앞서 구현한 탐색을 통해서 삽입하려는 값과 같은 값을 찾다가 실패하면 그 곳이 바로 삽입이 진행될 곳이다.
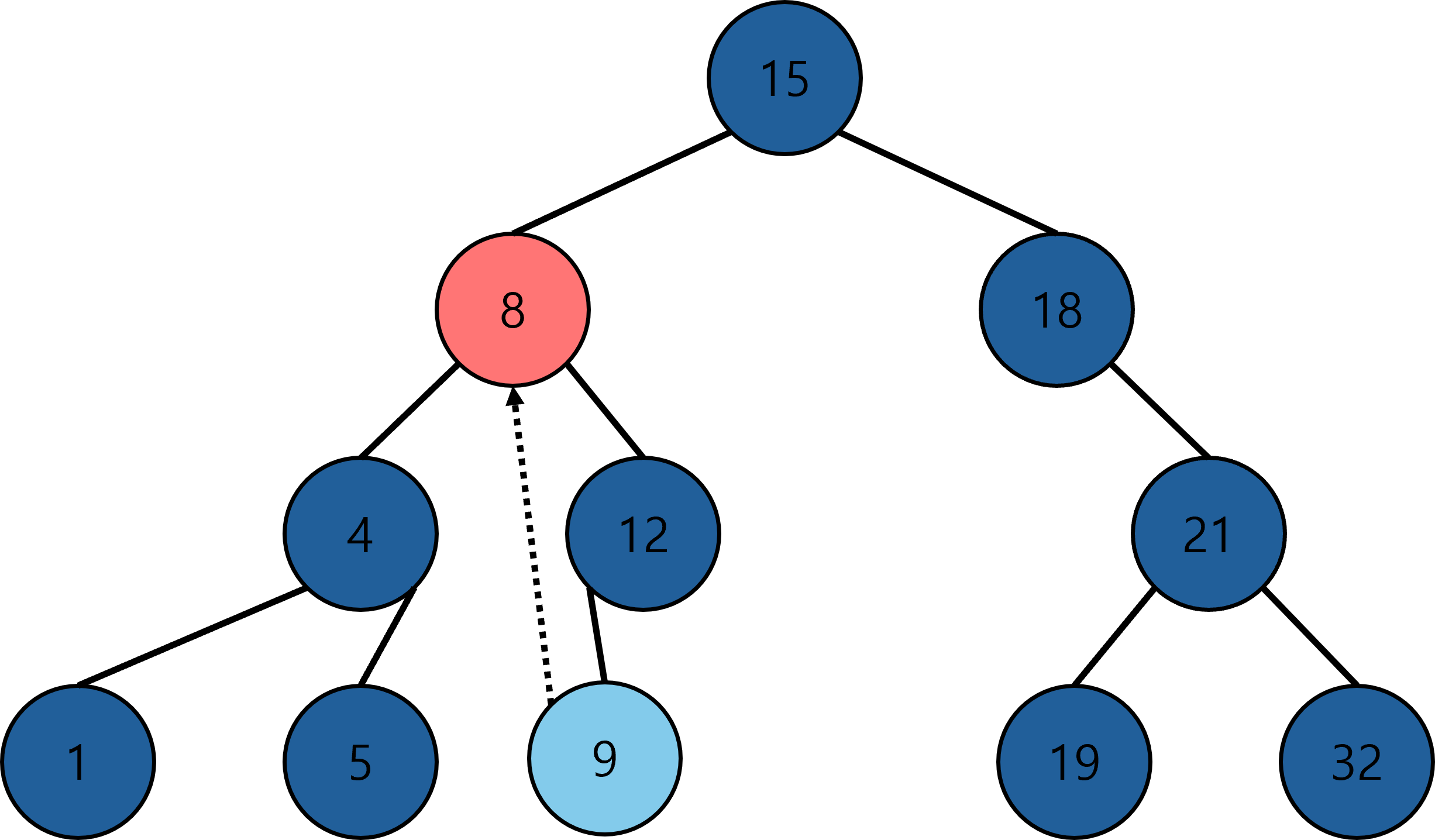
예를 들어 트리에 9를 삽입한다고 하면 아래와 같이 탐색할 것이다.

12의 왼쪽 서브트리에 9가 있어야 하는데 비어있으므로 9가 들어갈 자리가 된다. 따라서 다음과 같이 삽입된다.

구현은 다음과 같다.
TreeNode* insert_node(TreeNode* node, int key) {
if (node == NULL) {
return new_node(key);
}
if (key < node->data) {
node->left = insert_node(node->left, key);
} else if (key > node->data) {
node->right = insert_node(node->right, key);
}
return node;
}
TreeNode* new_node(int item) {
TreeNode* temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
삭제
삭제 연산은 좀 더 복잡하다. 세 가지 경우의 수가 존재하는데, 첫 번째로 삭제하려는 노드가 단말 노드인 경우, 두 번째로 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리를 가지고 있는 경우, 세 번째로 삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우이다.
첫 번째 경우인 단말 노드를 삭제하려는 경우 구현은 간단하다. 해당 단말 노드의 부모 노드를 찾아 연결을 끊고, 단말 노드의 할당된 메모리를 반환해주면 된다.

두 번째 경우인 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리를 가지고 있는 경우는 삭제하려는 노드의 부모 노드가 삭제하려는 노드를 가리키고 있던 것을 삭제하려는 노드의 서브 트리를 가리키게 만들면 된다. 그 후 삭제하려는 노드의 할당된 메모리를 반환하면 된다.


세 번째 경우인 두 개의 서브트리가 있는 경우 구현이 가장 복잡하다. 삭제하려는 노드를 삭제하고 해당 자리에 삭제하려는 노드가 가진 값과 가장 비슷한 값을 가진 노드를 불러와주어야 한다. 가장 비슷한 값을 찾는 것은 이진 탐색 트리의 특징을 이용하면 찾을 수 있다. 삭제하려는 노드의 왼쪽 서브트리의 가장 큰 값을 찾고, 오른쪽 서브 트리의 가장 작은 값을 찾아 비교하면 되기 때문이다.

구현은 다음과 같다. 세 번째 경우 오른쪽 서브 트리에서 가장 작은 값을 찾아 대체하였다.
TreeNode* delete_node(TreeNode* root, int key) {
if (root == NULL) {
return root;
}
if (key < root->data) {
root->left = delete_node(root->left, key);
} else if (key > root->data) {
root->right = delete_node(root->right, key);
} else {
if (root->left == NULL) {
TreeNode* temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
TreeNode* temp = root->left;
free(root);
return temp;
}
TreeNode* temp = root->right;
while (temp->left != NULL) {
temp = temp->left;
}
root->data = temp->data;
root->right = delete_node(root->right, temp->data);
}
return root;
}
시간복잡도
이진 탐색 트리에서의 탐색, 삽입, 삭제 연산의 시간복잡도는 트리의 높이에 비례한다.
최선의 경우는 이진 트리가 균형적으로 생성된 경우인데, 시간복잡도는 $ \mathcal{O}(\log n) $ 이다.
최악의 경우는 이진 트리가 한 쪽으로 치우친 경사 이진 트리인 경우인데, 시간복잡도는 $ \mathcal{O}(n) $ 이다.
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] 그래프(graph) (0) | 2024.11.18 |
|---|---|
| [Data Structure] 우선순위 큐(priority queue)와 힙(heap) (0) | 2024.11.17 |
| [Data Structure] 스레드 이진 트리(threaded binary tree) (0) | 2024.11.14 |
| [Data Structure] 이진 트리 순회(binary tree traversal) 및 활용 (0) | 2024.11.14 |
| [Data Structure] 트리(tree)와 이진 트리(binary tree) (0) | 2024.11.11 |