순회 (Traversal)
트리에서 순회란 트리의 노드들을 체계적으로 방문하는 것을 말한다. 기본적으로 세 가지 순회방법이 있는데, 전위순회, 중위순회, 후위순회이다. 왼쪽 서브트리를 L, 오른쪽 서브트리를 R, 루트 노드를 V라 하면 전위순회의 순회 순서는 VLR, 중위순회의 순서는 LVR, 후위순회의 순서는 LRV이다. 즉 V의 위치에 따라 전중후로 나눈다.
전중후 순회 외에 순회도 존재한다. 스택을 이용해 반복문으로 구현하는 반복적인 순회와 큐를 이용하여 구현하는 레벨 순회가 대표적이다.
각 순회들은 방문 방법만을 제시할 뿐 방문하여 어떤 연산을 할 것인지는 따로 구현하면 된다. 각 노드의 값을 출력할 수도 있고, 리스트를 만들어 리스트에 순회 순서대로 넣을 수도 있겠다.
이진트리 노드의 구조체는 아래와 같다고 가정한다.
typedef struct TreeNode {
int data;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
• 전위순회 (preorder traversal)
전위순회는 루트노드를 먼저 방문하고, 그 후 왼쪽 서브트리를 방문한 다음, 오른쪽 서브트리를 방문한다.
그림으로 본다면 아래와 같은 순서를 가진다.

전위순회를 이용하여 구조화된 문서 출력 등이 가능하다.
전위순회는 아래와 같이 구현된다. 방문한 노드의 데이터를 출력하는 코드이다.
void preorder_traversal(TreeNode* root) {
if (root) {
printf("%d", root->data);
preorder_traversal(root->left);
preorder_traversal(root->right);
}
}
• 중위순회 (inorder traversal)
중위순회는 왼쪽 서브트리를 먼저 방문하고, 그 후 루트 노드를 방문한 다음, 오른쪽 서브트리를 방문한다.
그림으로 본다면 아래와 같은 순서를 가진다.

중위순회를 이용하여 수식 트리를 계산 등이 가능하다.
중위순회는 아래와 같이 구현된다. 방문한 노드의 데이터를 출력하는 코드이다.
void inorder_traversal(TreeNode *root) {
if (root) {
inorder_traversal(root->left);
printf("%d", root->data);
inorder_traversal(root->right);
}
}
• 후위순회 (postorder traversal)
후위순회는 왼쪽 서브트리를 먼저 방문하고, 그 후 오른쪽 서브트리를 방문한 다음, 루트노드를 방문한다.
그림으로 본다면 아래와 같은 순서를 가진다.
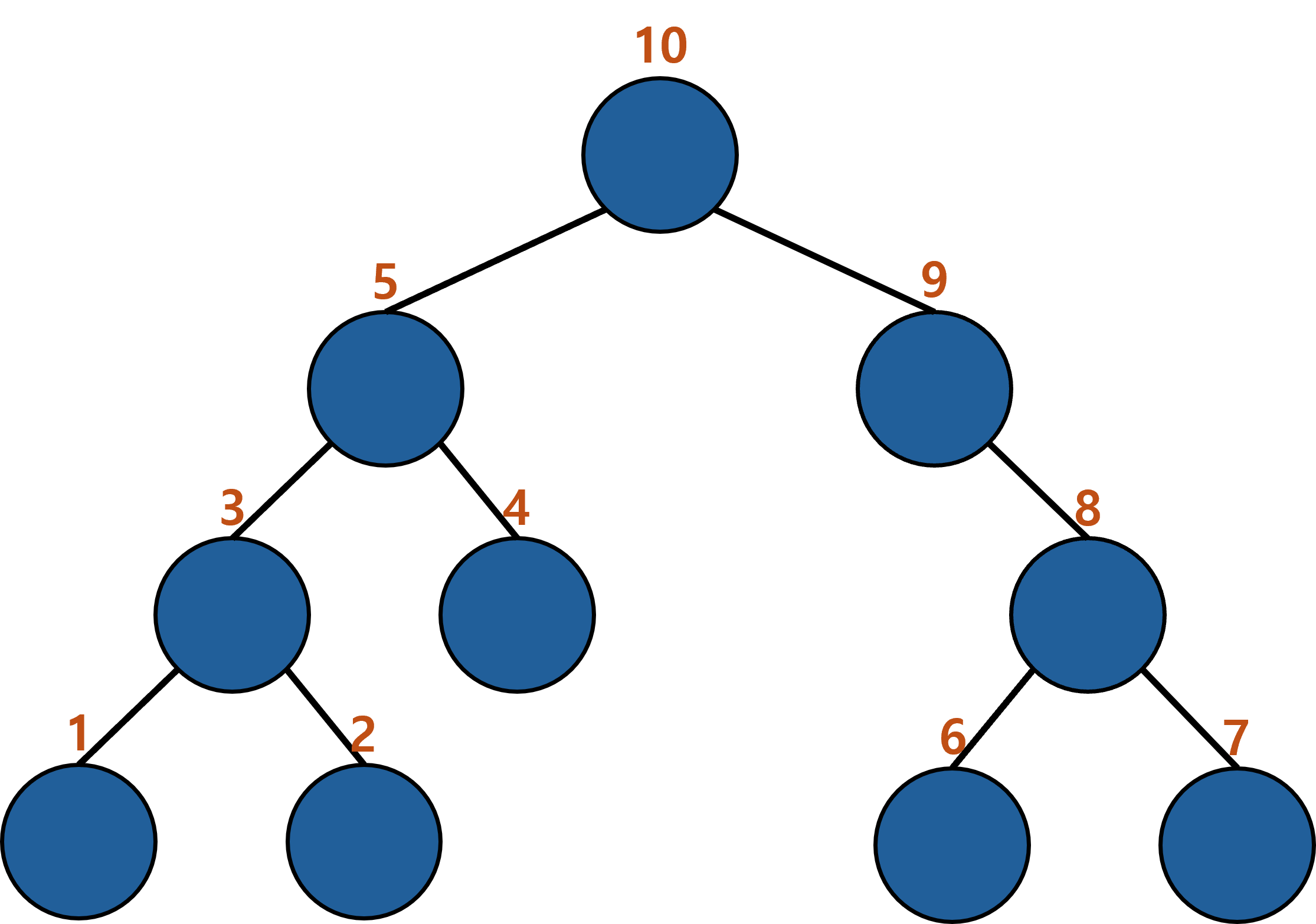
후위순회를 이용하여 디렉토리 용량 계산 등이 가능하고, 트리 선언하면서 트리 노드 초기화시에 후위순회로 출력되는 순서로 구현하면 트리 노드가 가리키는 노드 구현이 순차적으로 가능하다.
후위순회는 아래와 같이 구현된다. 방문한 노드의 데이터를 출력하는 코드이다.
void postorder_traversal(TreeNode *root) {
if (root) {
postorder_traversal(root->left);
postorder_traversal(root->right);
printf("%d", root->data);
}
}
• 반복적인 순회
반복적인 순회는 재귀함수가 아니라 반복문을 이용한 순회이다.
이때 스택을 활용하는데, 간단하게 아래와 같은 스택 구조체와 함수가 있다고 가정하자.
#define SIZE 100
typedef TreeNode* element;
typedef struct {
int top;
element data[SIZE];
} Stack;
void init(Stack* s) {
s->top = -1;
}
void push(Stack* s, element p)
{
if (s->top < SIZE - 1) {
s->data[++s->top] = p;
}
}
element pop(Stack* s)
{
if (s->top < 0) {
return NULL;
}
return s->data[s->top--];
}이제 반복문을 통해 중위순회를 아래와 같이 구현할 수 있다.
void inorder_traversal_iter(TreeNode *root) {
Stack s;
init(&s);
while (1) {
for (; root; root = root->left) {
push(&s, root);
}
push(&s, root);
root = pop(&s);
if (!root) {
break;
}
printf("%d", root->data);
root = root->right;
}
}응용하면 전위, 후위순회도 구현 가능하다.
• 레벨 순회 (level order traversal)
각 노드를 레벨 순으로 방문하는 순회이다.
그림으로 본다면 아래와 같은 순서를 가진다.

앞서 반복적인 순회에서는 스택을 활용했다면 레벨 순회에서는 큐를 활용한다. 간단하게 아래와 같은 큐 구조체와 함수가 있다고 가정하자.
#define SIZE 100
typedef TreeNode* element;
typedef struct {
element data[SIZE];
int front;
int rear;
} Queue;
void init_queue(Queue* q) {
q->front = q->rear = 0;
}
int is_empty(Queue* q) {
return (q->front == q->rear);
}
int is_full(Queue* q) {
return ((q->rear + 1) % SIZE == q->front);
}
void enqueue(Queue* q, element item) {
if (is_full(q)) {
return;
}
q->rear = (q->rear + 1) % SIZE;
q->data[q->rear] = item;
}
element dequeue(Queue* q) {
if (is_empty(q)) {
return NULL;
}
q->front = (q->front + 1) % SIZE;
return q->data[q->front];
}이제 큐를 활용한 레벨 순회를 아래와 같이 구현할 수 있다.
void level_order_traversal(TreeNode* ptr) {
Queue q;
init_queue(&q);
if (ptr == NULL) {
return;
}
enqueue(&q, ptr);
while (!is_empty(&q)) {
ptr = dequeue(&q);
printf("%d", ptr->data);
if (ptr->left) {
enqueue(&q, ptr->left);
}
if (ptr->right) {
enqueue(&q, ptr->right);
}
}
}
노드 개수 확인
탐색 대상 트리의 노드 개수를 계산하여 반환하는 함수이다.
각각의 서브트리에 대하여 순환 호출을 하여 반환되는 값에 1을 더하여 다시 반환하는 방식으로 구현된다.
int get_size(TreeNode* node) {
if (node) {
return 1 + get_size(node->left) + get_size(node->right);
} else {
return 0;
}
}
높이 확인
서브트리에 대하여 순환 호출하여 서브트리들의 반환값 중에서 최대값을 구한 후 1을 더하여 다시 반환하는 방식으로 구현한다.
int get_height(TreeNode* node) {
if (node) {
return 1 + max(get_height(node->left), get_height(node->right));
} else {
return 0;
}
}
단말 노드 개수 확인
응용하여 단말 노드 개수도 확인 가능하다.
int get_leaf_count(TreeNode* node) {
if (node) {
if (node->left == NULL && node->right == NULL) {
return 1;
} else {
return get_leaf_count(node->left) + get_leaf_count(node->right);
}
}
return 0;
}
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] 이진 탐색 트리(binary search tree) (0) | 2024.11.14 |
|---|---|
| [Data Structure] 스레드 이진 트리(threaded binary tree) (0) | 2024.11.14 |
| [Data Structure] 트리(tree)와 이진 트리(binary tree) (0) | 2024.11.11 |
| [Data Structure] 연결 리스트를 통한 스택과 큐 구현 (0) | 2024.11.02 |
| [Data Structure] 이중 연결 리스트(doubly linked list) (0) | 2024.11.02 |