이진 트리
이진 트리는 각 정점의 자식의 수가 최대 2개인 트리이다. 이때 자식은 왼쪽 자식 혹은 오른쪽 자식으로 지정된다.
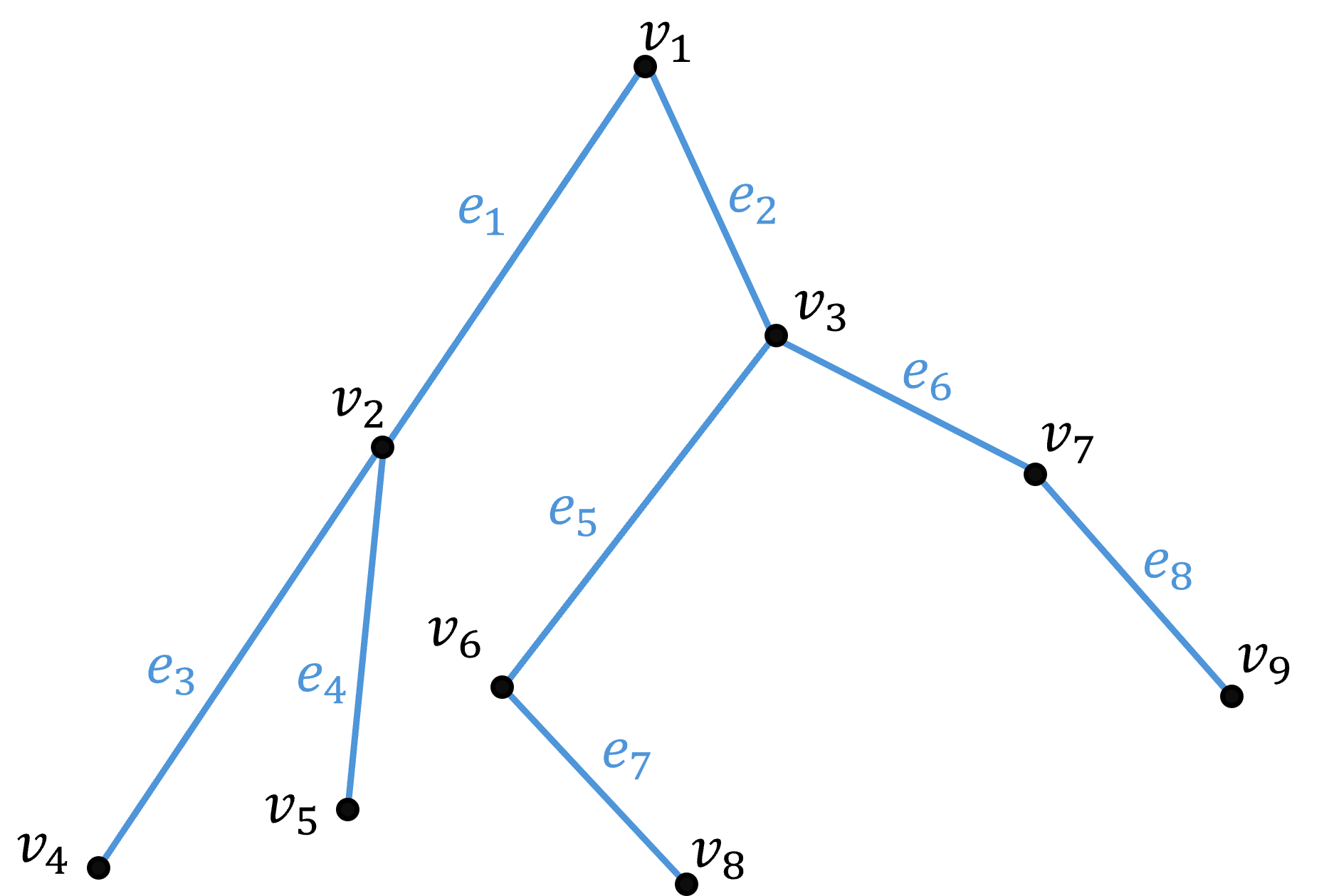
트리 운행
트리의 각 정점을 정확히 한 번씩 방분하는 체계적 방법으로 트리를 운행한다. 순회라고도 한다.
이진 트리에서 운행은 전위 운행법(preorder traversal), 중위 운행법(inorder traversal), 후위 운행법(postorder traversal)이 존재한다. 전위, 중위, 후위에서 전, 중, 후는 운행 중 루트의 위치를 말한다. 전위는 루트를 먼저 처리하고, 중위는 중간에, 후위는 마지막에 처리한다.
- 전위 운행법
입력: $ T $ (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: $ \text{process} $ 에 따라 종속적
preorder(T) {
if (T = NULL) {
return
}
process(T)
preorder(T.left)
preorder(T.right)
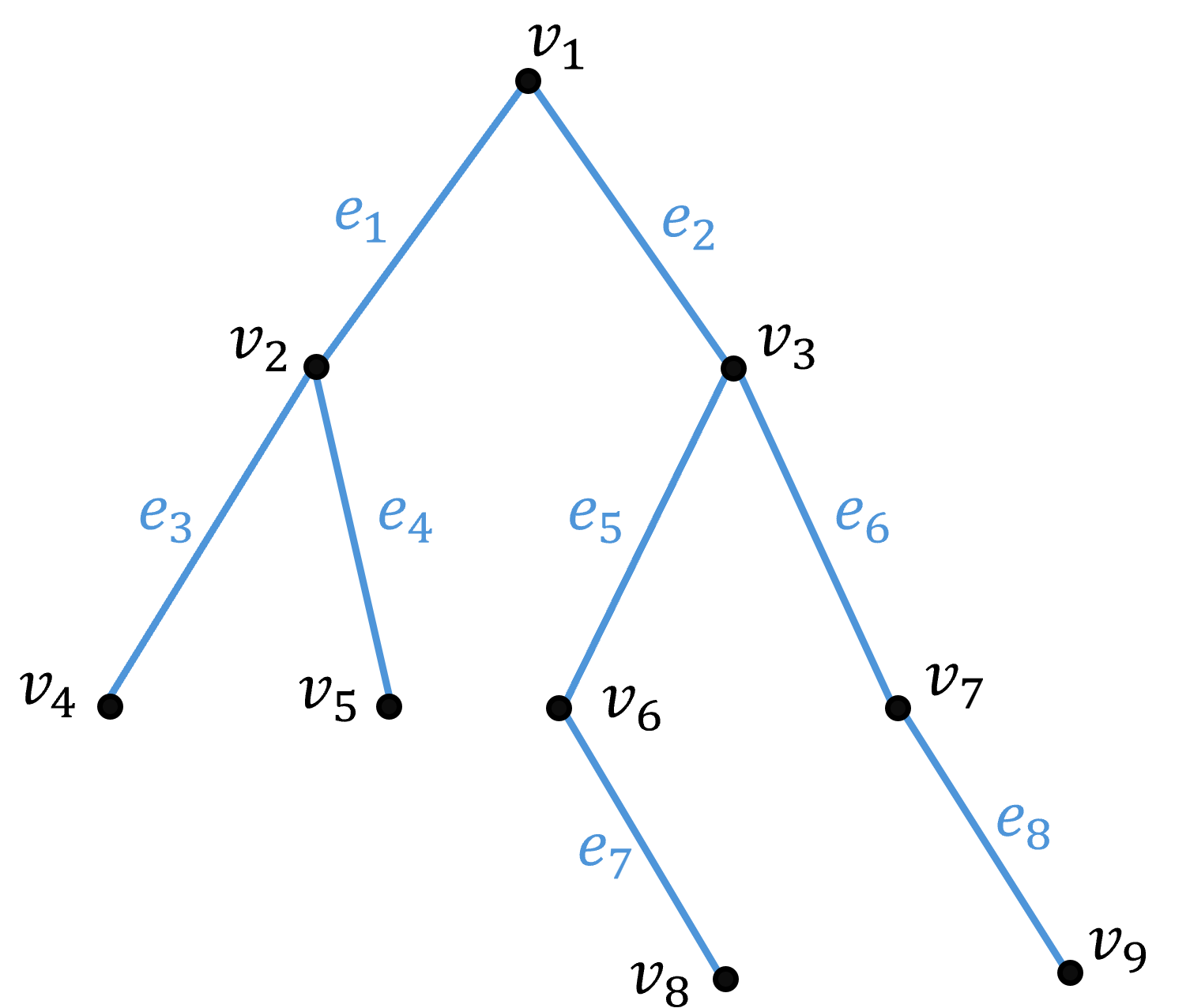
}위 트리를 전위 운행법으로 운행하면 $ v_1 \to v_2 \to v_4 \to v_5 \to v_3 \to v_6 \to v_8 \to v_7 \to v_9 $ 으로 순행한다.
- 중위 운행법
입력: $ T $ (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: $ \text{process} $ 에 따라 종속적
inorder(T) {
if (T = NULL) {
return
}
inorder(T.left)
process(T)
inorder(T.right)
}위 트리를 중위 운행법으로 운행하면 $ v_4 \to v_2 \to v_5 \to v_1 \to v_6 \to v_8 \to v_3 \to v_7 \to v_9 $ 으로 순행한다.
- 후위 운행법
입력: $ T $ (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: $ \text{process} $ 에 따라 종속적
postorder(T) {
if (T = NULL) {
return
}
postorder(T.left)
postorder(T.right)
process(T)
}위 트리를 후위 운행법으로 운행하면 $ v_4 \to v_5 \to v_2 \to v_8 \to v_6 \to v_9 \to v_7 \to v_3 \to v_1 $ 으로 순행한다.
이진 트리로 수식 표현
산술 수식을 이진 트리로 표현하는 방법이다. 말단 정점이 피연산자(operands)이고 중간 정점이 연산자(operators)이다.
예를 들어 $ (A + B) * C - D / E $ 를 이진 트리로 표현하면 아래와 같다.

이를 후위 운행법으로 방문하면 $ AB+C*DE/- $ 가 나오는데 이것은 수식의 후위 표기법이다. 연산자가 피연산자보다 뒤에 나오고 괄호가 필요없다는 장점이 있다. 컴퓨터에서 수식을 처리할 때 후위 표기법으로 처리한다.
'Mathematics > Discrete Mathematics' 카테고리의 다른 글
| [Discrete Mathematics] 결정 트리(decision tree) 및 최소 시간 (0) | 2024.11.30 |
|---|---|
| [Discrete Mathematics] 신장 트리(spanning tree) 및 최소 신장 트리(minimal spanning tree) (0) | 2024.11.29 |
| [Discrete Mathematics] 트리(tree)와 허프만 코드(Huffman codes) (0) | 2024.11.27 |
| [Discrete Mathematics] 그래프 동형사상(isomorphism of graph) 및 위상동형(homeomorphic) (0) | 2024.11.21 |
| [DIscrete Mathematics] 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2024.11.20 |
이진 트리
이진 트리는 각 정점의 자식의 수가 최대 2개인 트리이다. 이때 자식은 왼쪽 자식 혹은 오른쪽 자식으로 지정된다.

트리 운행
트리의 각 정점을 정확히 한 번씩 방분하는 체계적 방법으로 트리를 운행한다. 순회라고도 한다.
이진 트리에서 운행은 전위 운행법(preorder traversal), 중위 운행법(inorder traversal), 후위 운행법(postorder traversal)이 존재한다. 전위, 중위, 후위에서 전, 중, 후는 운행 중 루트의 위치를 말한다. 전위는 루트를 먼저 처리하고, 중위는 중간에, 후위는 마지막에 처리한다.

- 전위 운행법
입력: TT (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: processprocess 에 따라 종속적
preorder(T) {
if (T = NULL) {
return
}
process(T)
preorder(T.left)
preorder(T.right)
}위 트리를 전위 운행법으로 운행하면 v1→v2→v4→v5→v3→v6→v8→v7→v9v1→v2→v4→v5→v3→v6→v8→v7→v9 으로 순행한다.
- 중위 운행법
입력: TT (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: processprocess 에 따라 종속적
inorder(T) {
if (T = NULL) {
return
}
inorder(T.left)
process(T)
inorder(T.right)
}위 트리를 중위 운행법으로 운행하면 v4→v2→v5→v1→v6→v8→v3→v7→v9v4→v2→v5→v1→v6→v8→v3→v7→v9 으로 순행한다.
- 후위 운행법
입력: TT (이진 트리의 루트 혹은 트리가 비어있음을 나타내는 NULL)
출력: processprocess 에 따라 종속적
postorder(T) {
if (T = NULL) {
return
}
postorder(T.left)
postorder(T.right)
process(T)
}위 트리를 후위 운행법으로 운행하면 v4→v5→v2→v8→v6→v9→v7→v3→v1v4→v5→v2→v8→v6→v9→v7→v3→v1 으로 순행한다.
이진 트리로 수식 표현
산술 수식을 이진 트리로 표현하는 방법이다. 말단 정점이 피연산자(operands)이고 중간 정점이 연산자(operators)이다.
예를 들어 (A+B)∗C−D/E(A+B)∗C−D/E 를 이진 트리로 표현하면 아래와 같다.

이를 후위 운행법으로 방문하면 AB+C∗DE/−AB+C∗DE/− 가 나오는데 이것은 수식의 후위 표기법이다. 연산자가 피연산자보다 뒤에 나오고 괄호가 필요없다는 장점이 있다. 컴퓨터에서 수식을 처리할 때 후위 표기법으로 처리한다.
'Mathematics > Discrete Mathematics' 카테고리의 다른 글
| [Discrete Mathematics] 결정 트리(decision tree) 및 최소 시간 (0) | 2024.11.30 |
|---|---|
| [Discrete Mathematics] 신장 트리(spanning tree) 및 최소 신장 트리(minimal spanning tree) (0) | 2024.11.29 |
| [Discrete Mathematics] 트리(tree)와 허프만 코드(Huffman codes) (0) | 2024.11.27 |
| [Discrete Mathematics] 그래프 동형사상(isomorphism of graph) 및 위상동형(homeomorphic) (0) | 2024.11.21 |
| [DIscrete Mathematics] 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2024.11.20 |