그래프 동형사상
어떤 두 그래프가 겉보기에는 완전히 다른 그래프처럼 보이지만, 구조만 때어놓고 본다면 같은 구조를 가진 그래프일 수 있다. 아래 그래프를 보면 정점과 간선의 이름, 생김새가 다르게 보인다.
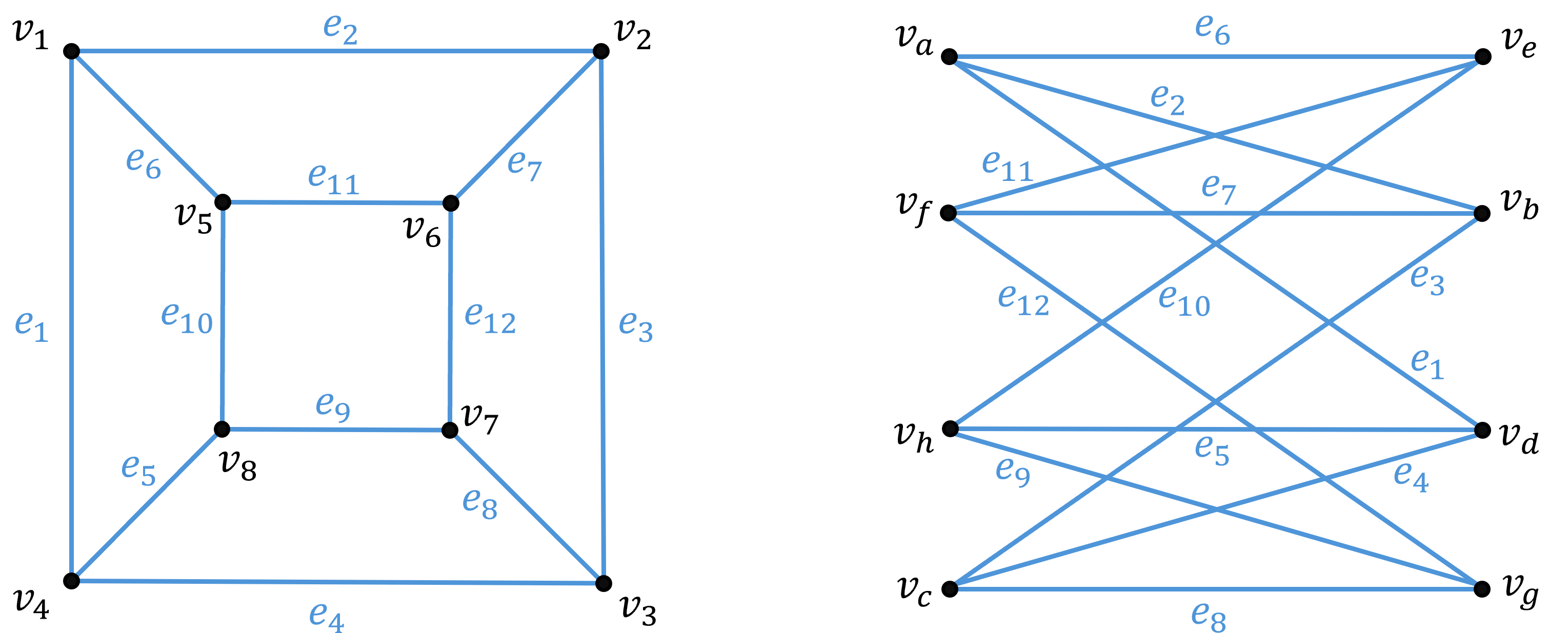
그러나 재배열 한다면 비슷한 그래프처럼 보인다.
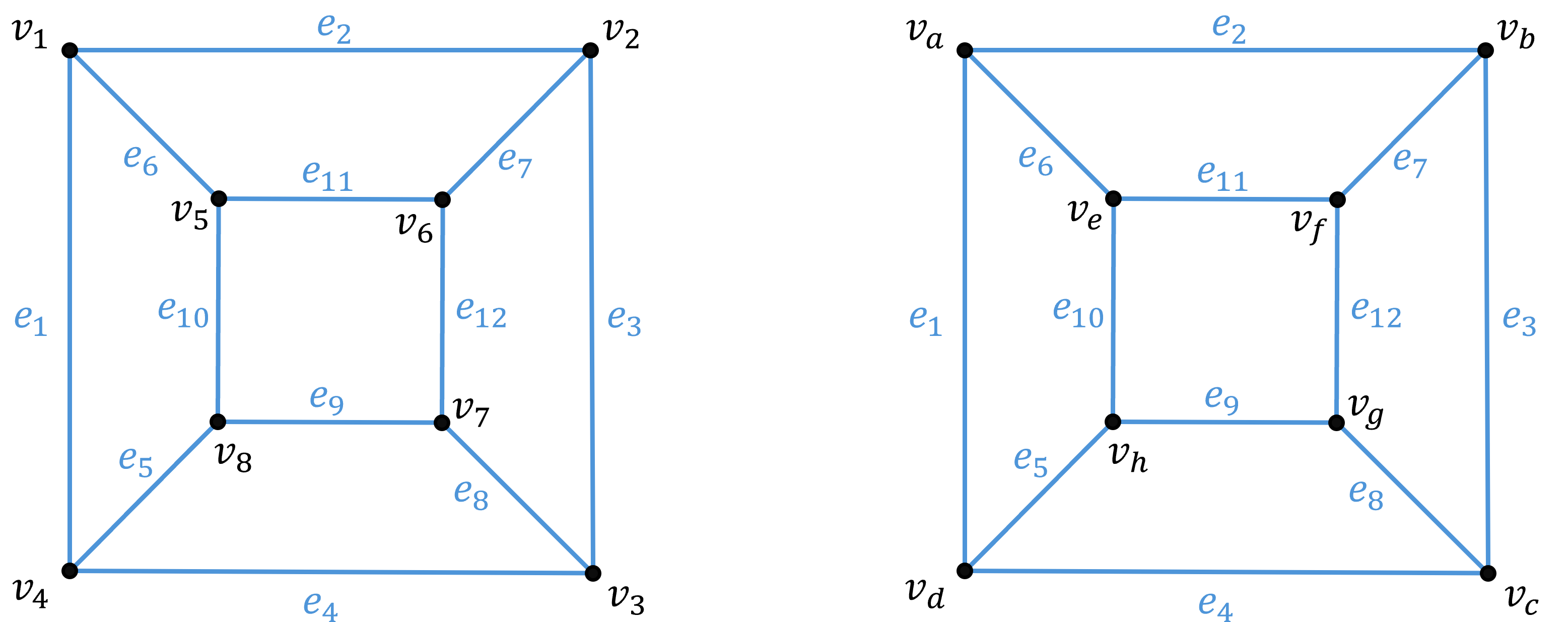
이처럼 구조가 같은 그래프를 동형이라 한다. 좀더 명확하게는 다음과 같이 정의힌다.
그래프 $ G_1 = (V_1, E_1) $ 과 그래프 $ G_2 = (V_2, E_2) $ 가 동형(isomorphic)이라 할 때 다음 조건을 만족하는 함수 쌍 $ f $ 와 $ g $ 가 존재하고, 이를 동형사상(혹은 동형함수)이라 한다.
$ f: V_1 \to V_2 $ 와 $ g: E_1 \to E_2 $ 는 전단사 함수이다. 즉 $ f $ 는 $ V_1 $ 의 모든 정점을 $ V_2 $ 의 정점으로 매핑하고, 각 정점은 유일한 대응 관계를 가지며, $g $ 는 $ E_1 $ 의 모든 간선을 $ E_2 $ 의 모든 간선으로 매핑하고, 각 간선은 유일한 대응 관계를 가진다. 또한 $ G_1 $ 의 간선 $ e \in E_1 $ 이 $ G_1 $ 의 정점 $ v, w \in V_1 $ 을 연결할 때 $ G_2 $ 의 간선 $ g(e) \in E_2 $ 는 반드시 $ G_2 $ 의 정점 $ f(v), f(w) \in V_2 $ 를 연결해야 한다.
평면 그래프 (Planar Graph)
평면 상에 그래프를 그렸을 때, 간선이 정점 외에서는 만나지 않도록 그릴 수 있는 그래프를 평면(planar)이라 한다. 이러한 평면이 연결 그래프라면 그 평면은 면(face)이라는 연속된 영역으로 나눠진다. 면은 그 경계를 형성하는 사이클에 의해 규정된다. 면의 수 $ f $ 는 정점의 수가 $ v $, 간선의 수가 $ e $ 라 할 때 $ f = e - v + 2 $ 이다.
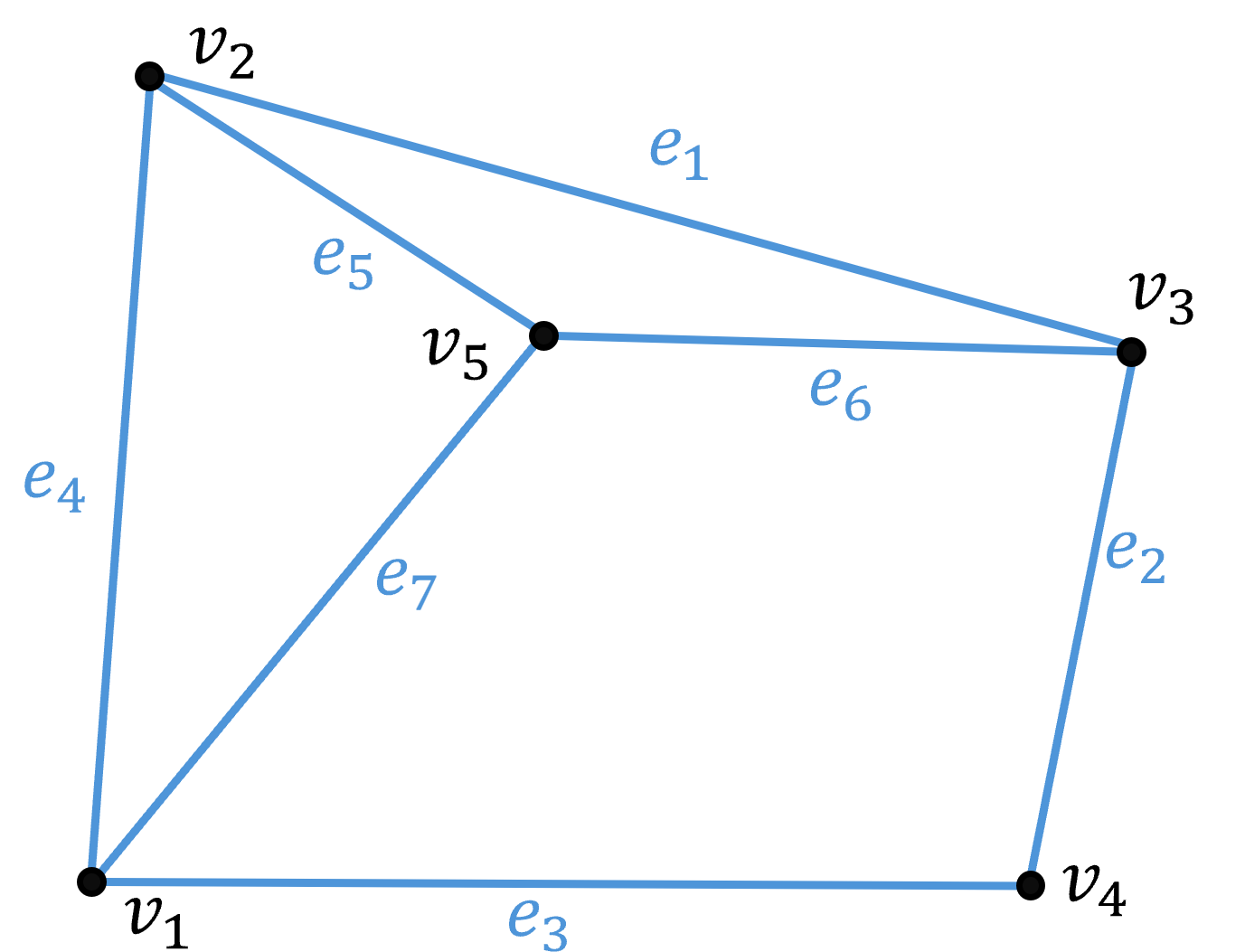
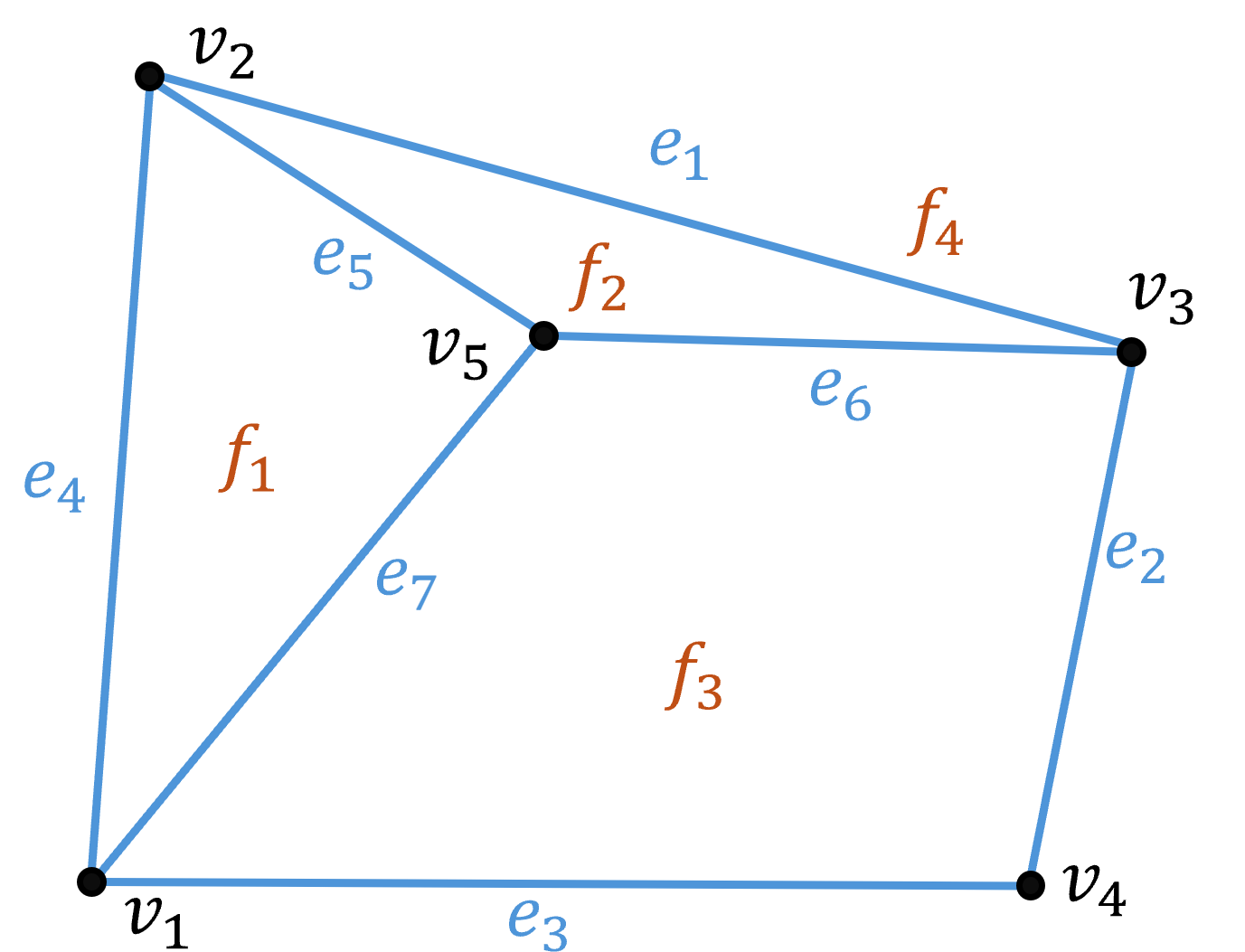
위와 같은 평면 그래프가 있다고 가정할 때 간선의 수 $ e = 7 $, 정점의 수 $ v = 5 $ 이므로 면의 수 $ f = 4 $ 이다. 안의 면 3개와 바깥을 면으로 보기 때문에 1개로 총 4개가 맞다.
그래프 위상동형
어떤 그래프 $ G $ 가 차수가 2인 정점 $ v $ 와 $ v_1 \neq v_2 $ 인 $ (v, v_1) $, $ (v, v_2 ) $ 를 가진다 할 때 간선 $ (v, v_1) $, $(v, v_2) $ 는 시리즈(series) 안에 있다고 한다. 아래와 같은 그래프의 $ v, v_1, v_2 $ 를 상정하면 된다.
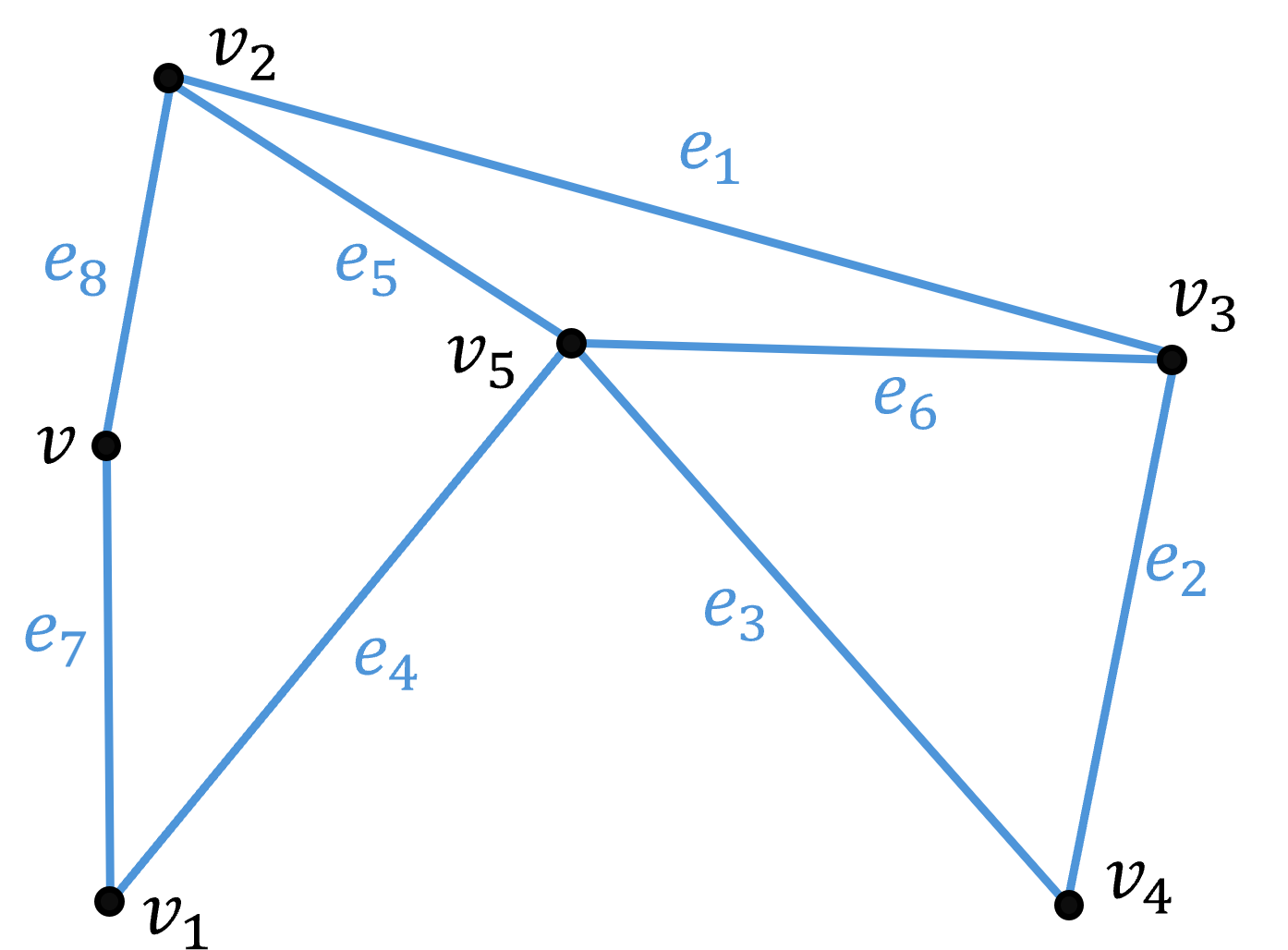
시리즈 축소(series reduction)는 위에서 말한 시리즈 안에 있는 간선 $ (v, v_1 ) $ 과 $ (v, v_2) $ 를 간선 $ v_1, v_2) $ 로 대채하는 것으로 정점 $ v $ 가 제거되는 것이다. 이를 통해 얻어진 그래프 $ G^\prime $ 은 $ G $ 로부터 시리즈 축소에 의해 얻을 수 있다고 말한다. 편의상 $ G $ 는 그자체로부터 시리즈 축소에 의해 얻을 수 있다고 간주한다.
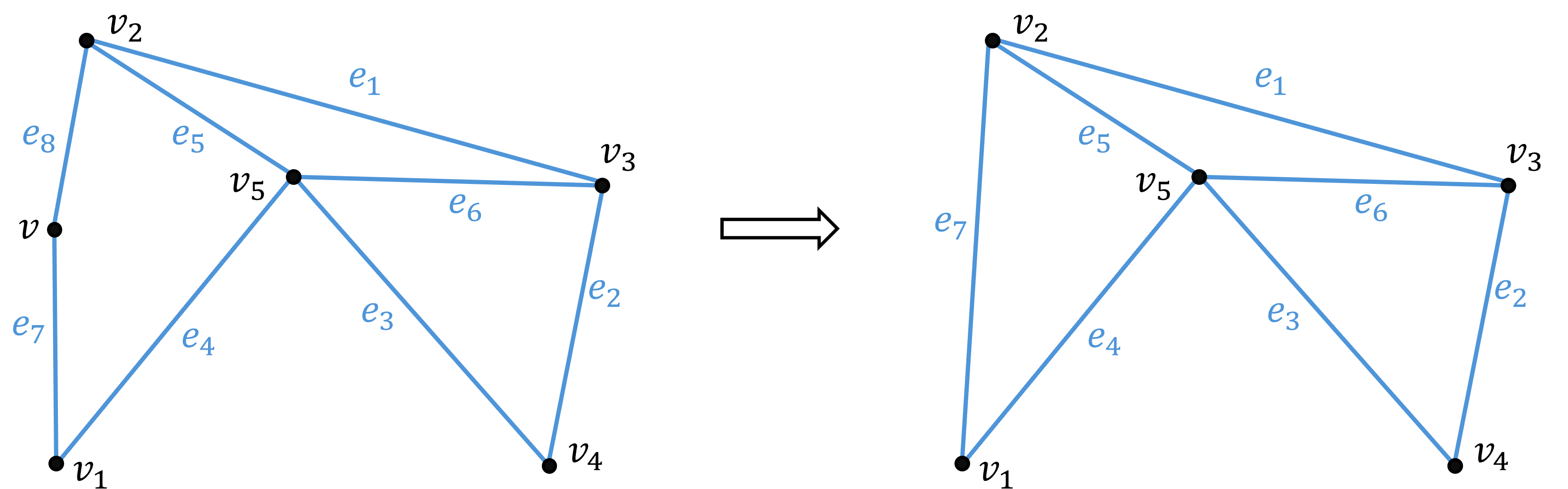
만약 그래프 $ G_1, G_2 $ 가 일련의 시리즈 축소를 통해 동형인 그래프로 축소될 수 있다면, 이 그래프 $ G_1, G_2 $ 를 위상동형(homeomorphic) 혹은 동상이라 한다.
쿠라토프스키의 정리(Kuratowski’s theorem)은 어떤 그래프 $ G $ 가 평면 그래프일 필요충분조건이 $ G $ 는 $ K_5 $ 또는 $ K_{3, 3} $ 에 동상인 부분 그래프를 포함하지 않아야 한다는 것을 말한다.
오일러 공식
어떤 연결된 평면 그래프 $ G $ 의 간선의 수가 $ e $, 정점의 수가 $ v $, 면의 수가 $ f $ 라 하면 $ f = e - v + 2 $ 이다. 이에 대한 증명은 간선의 수에 대한 귀납 방법을 사용한다.
$ e = 1 $ 이라고 가정하면 $ G $ 는 다음 두 그래프 중 하나이다.

따라서 첫번째 그래프인 경우 $ f = 1, e = 1, v= 2$ 이므로 성립하고, 두번째 그래프인 경우 $ f = 2, e = 1, v = 1 $ 이므로 성립한다. 이로써 기본단계 증명이 끝난다.
이 공식이 $ n $ 개의 간선을 가지는 연결된 평면 그래프에서 성립한다고 가정하자. $ G $ 가 $ n+1 $ 개의 간선을 가지고, 사이클이 없을 때, 정점 $ v $ 를 선택하고 $ v $ 에서 출발하여 하나의 경로를 추적하면 $ G $ 가 사이클이 없으므로 간선을 추적할 때마다 새로운 정점에 도달 가능하다. 결국 차수가 1인 어떤 정점 $ \alpha $ 에 도착할 것이고, 이 정점에서 나갈 수 없다. 그렇다면 $ \alpha $ 를 제거하고 $ \alpha$ 에 결합된 간선 $ x $ 를 제거하여 그래프 $ G^\prime $ 을 얻을 수 있는데, 이 그래프 $ G^\prime $ 은 $ n $ 개의 간선을 가지고 연결되어 있고, 따라서 앞선 가정에 의해 이 공식이 성립한다. $ G $ 는 $ G^\prime $ 보다 간선이 하나, 정점이 하나 많고 면의 수가 같으므로 $ G $ 역시 이 공식이 성립한다.
만약 $ G $ 가 $ n + 1 $ 개의 간선을 가지고, 사이클을 포함한다 가정하면, 그리고 $ x $ 를 사이클 안의 한 간선이라 가정하면 $ x $ 는 두 면의 경계의 한 부분이다. 정점의 제거 없이 간선 $ x $ 를 제거하여 그래프 $ G^\prime $ 을 얻는다면 $ G ^\prime $ 은 $ n $ 개의 간선을 가지고 연결되어 있는 평면 그래프이다. 즉 수학적 귀납법 가정에 의해 $ G^\prime $ 에 대해 이 공식이 성립한다. $ G $ 는 $ G^\prime $ 보다 면이 하나, 간선이 하나 많고, 정점의 수가 같으므로 $ G $ 역시 이 공식이 성립한다.
기본단계와 귀납단계의 증명이 끝났으므로 귀납원리에 의해 앞선 정리, 어떤 연결된 평면 그래프 $ G $ 의 간선의 수가 $ e $, 정점의 수가 $ v $, 면의 수가 $ f $ 라 하면 $ f = e - v + 2 $ 이다는 증명된다.
'Mathematics > Discrete Mathematics' 카테고리의 다른 글
| [Discrete Mathematics] 신장 트리(spanning tree) 및 최소 신장 트리(minimal spanning tree) (0) | 2024.11.29 |
|---|---|
| [Discrete Mathematics] 트리(tree)와 허프만 코드(Huffman codes) (0) | 2024.11.27 |
| [DIscrete Mathematics] 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2024.11.20 |
| [Discrete Mathematics] 오일러 사이클(Euler cycle) 및 해밀턴 사이클(Hamiltonian cycle) (0) | 2024.11.19 |
| [Discrete Mathematics] 그래프(graph)의 기본 개념과 그래프 구분 (0) | 2024.11.19 |
그래프 동형사상
어떤 두 그래프가 겉보기에는 완전히 다른 그래프처럼 보이지만, 구조만 때어놓고 본다면 같은 구조를 가진 그래프일 수 있다. 아래 그래프를 보면 정점과 간선의 이름, 생김새가 다르게 보인다.

그러나 재배열 한다면 비슷한 그래프처럼 보인다.

이처럼 구조가 같은 그래프를 동형이라 한다. 좀더 명확하게는 다음과 같이 정의힌다.
그래프 G1=(V1,E1)G1=(V1,E1) 과 그래프 G2=(V2,E2)G2=(V2,E2) 가 동형(isomorphic)이라 할 때 다음 조건을 만족하는 함수 쌍 ff 와 gg 가 존재하고, 이를 동형사상(혹은 동형함수)이라 한다.
f:V1→V2f:V1→V2 와 g:E1→E2g:E1→E2 는 전단사 함수이다. 즉 ff 는 V1V1 의 모든 정점을 V2V2 의 정점으로 매핑하고, 각 정점은 유일한 대응 관계를 가지며, gg 는 E1E1 의 모든 간선을 E2E2 의 모든 간선으로 매핑하고, 각 간선은 유일한 대응 관계를 가진다. 또한 G1G1 의 간선 e∈E1e∈E1 이 G1G1 의 정점 v,w∈V1v,w∈V1 을 연결할 때 G2G2 의 간선 g(e)∈E2g(e)∈E2 는 반드시 G2G2 의 정점 f(v),f(w)∈V2f(v),f(w)∈V2 를 연결해야 한다.
평면 그래프 (Planar Graph)
평면 상에 그래프를 그렸을 때, 간선이 정점 외에서는 만나지 않도록 그릴 수 있는 그래프를 평면(planar)이라 한다. 이러한 평면이 연결 그래프라면 그 평면은 면(face)이라는 연속된 영역으로 나눠진다. 면은 그 경계를 형성하는 사이클에 의해 규정된다. 면의 수 ff 는 정점의 수가 vv, 간선의 수가 ee 라 할 때 f=e−v+2f=e−v+2 이다.

위와 같은 평면 그래프가 있다고 가정할 때 간선의 수 e=7e=7, 정점의 수 v=5v=5 이므로 면의 수 f=4f=4 이다. 안의 면 3개와 바깥을 면으로 보기 때문에 1개로 총 4개가 맞다.

그래프 위상동형
어떤 그래프 GG 가 차수가 2인 정점 vv 와 v1≠v2v1≠v2 인 (v,v1)(v,v1), (v,v2)(v,v2) 를 가진다 할 때 간선 (v,v1)(v,v1), (v,v2)(v,v2) 는 시리즈(series) 안에 있다고 한다. 아래와 같은 그래프의 v,v1,v2v,v1,v2 를 상정하면 된다.

시리즈 축소(series reduction)는 위에서 말한 시리즈 안에 있는 간선 (v,v1)(v,v1) 과 (v,v2)(v,v2) 를 간선 v1,v2)v1,v2) 로 대채하는 것으로 정점 vv 가 제거되는 것이다. 이를 통해 얻어진 그래프 G′ 은 G 로부터 시리즈 축소에 의해 얻을 수 있다고 말한다. 편의상 G 는 그자체로부터 시리즈 축소에 의해 얻을 수 있다고 간주한다.

만약 그래프 G1,G2 가 일련의 시리즈 축소를 통해 동형인 그래프로 축소될 수 있다면, 이 그래프 G1,G2 를 위상동형(homeomorphic) 혹은 동상이라 한다.
쿠라토프스키의 정리(Kuratowski’s theorem)은 어떤 그래프 G 가 평면 그래프일 필요충분조건이 G 는 K5 또는 K3,3 에 동상인 부분 그래프를 포함하지 않아야 한다는 것을 말한다.
오일러 공식
어떤 연결된 평면 그래프 G 의 간선의 수가 e, 정점의 수가 v, 면의 수가 f 라 하면 f=e−v+2 이다. 이에 대한 증명은 간선의 수에 대한 귀납 방법을 사용한다.
e=1 이라고 가정하면 G 는 다음 두 그래프 중 하나이다.

따라서 첫번째 그래프인 경우 f=1,e=1,v=2 이므로 성립하고, 두번째 그래프인 경우 f=2,e=1,v=1 이므로 성립한다. 이로써 기본단계 증명이 끝난다.
이 공식이 n 개의 간선을 가지는 연결된 평면 그래프에서 성립한다고 가정하자. G 가 n+1 개의 간선을 가지고, 사이클이 없을 때, 정점 v 를 선택하고 v 에서 출발하여 하나의 경로를 추적하면 G 가 사이클이 없으므로 간선을 추적할 때마다 새로운 정점에 도달 가능하다. 결국 차수가 1인 어떤 정점 α 에 도착할 것이고, 이 정점에서 나갈 수 없다. 그렇다면 α 를 제거하고 α 에 결합된 간선 x 를 제거하여 그래프 G′ 을 얻을 수 있는데, 이 그래프 G′ 은 n 개의 간선을 가지고 연결되어 있고, 따라서 앞선 가정에 의해 이 공식이 성립한다. G 는 G′ 보다 간선이 하나, 정점이 하나 많고 면의 수가 같으므로 G 역시 이 공식이 성립한다.
만약 G 가 n+1 개의 간선을 가지고, 사이클을 포함한다 가정하면, 그리고 x 를 사이클 안의 한 간선이라 가정하면 x 는 두 면의 경계의 한 부분이다. 정점의 제거 없이 간선 x 를 제거하여 그래프 G′ 을 얻는다면 G′ 은 n 개의 간선을 가지고 연결되어 있는 평면 그래프이다. 즉 수학적 귀납법 가정에 의해 G′ 에 대해 이 공식이 성립한다. G 는 G′ 보다 면이 하나, 간선이 하나 많고, 정점의 수가 같으므로 G 역시 이 공식이 성립한다.
기본단계와 귀납단계의 증명이 끝났으므로 귀납원리에 의해 앞선 정리, 어떤 연결된 평면 그래프 G 의 간선의 수가 e, 정점의 수가 v, 면의 수가 f 라 하면 f=e−v+2 이다는 증명된다.
'Mathematics > Discrete Mathematics' 카테고리의 다른 글
| [Discrete Mathematics] 신장 트리(spanning tree) 및 최소 신장 트리(minimal spanning tree) (0) | 2024.11.29 |
|---|---|
| [Discrete Mathematics] 트리(tree)와 허프만 코드(Huffman codes) (0) | 2024.11.27 |
| [DIscrete Mathematics] 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2024.11.20 |
| [Discrete Mathematics] 오일러 사이클(Euler cycle) 및 해밀턴 사이클(Hamiltonian cycle) (0) | 2024.11.19 |
| [Discrete Mathematics] 그래프(graph)의 기본 개념과 그래프 구분 (0) | 2024.11.19 |