[Descriptive Statistics] 자료의 종류와 요약 및 시각화

---

모집단과 표본

 

• 모집단 (Popuation)

관심의 대상이 되는 모든 개체의 집합 혹은 확률모형을 말한다. 모집단을 구성하는 개체의 수가 유한할 경우 유한모집단, 무한할 경우 무한모집단이라 한다.

• 표본 (Sample)

모집단의 일부로서 실제 조사되는 대상의 집합이다. 확률변수 혹은 확률벡터들의 집합으로 이해할 수 있다.

• 전수조사 (Census)

모집단 전체를 조사하는 것이다. 단 조사비용, 시간 등의 문제와 조사과정에서 발생할 수 있는 비표본오차 증가 가능성, 조사 시간에 변화를 측정하지 못하는 문제 등이 있다.

• 표본조사 (Sample Survey)

모집단의 일부인 표본을 조사하는 것이다. 경제성, 신속성, 정확성, 필요성, 대표성, 적절성을 가지지만, 모집단을 대표하지 못하는 잘못된 표본을 조사할 경우 잘못된 통계를 만들 수 있다. 또한 모집단 내 희소한 집단의 특성까지 조사하는 데에는 어려움이 있다.

• 모수 (Parameter)

모집단에서 얻어지는 수치적 특성이다.

• $ \mu $ | 모평균
• $ \sigma^2 $ | 모분산
• $ P $ | 모비율
• $ N $ | 모집단의 크기

• 통계량 (Statistic)

표본에서 얻어지는 수치적 특성이다. 즉 표본들의 함수로 표본의 관측값(observation)들이 주어지면 계산 가능하다. 표본들의 함수라는 것은 확률변수라는 말이기도 하다. 모수 추론에 사용된다.

• $ \bar{X} $ | 표본평균
• $ S^2 $ | 표본분산
• $ \hat{P} $ | 표본비율
• $ n $ | 표본의 크기

• 통계값 혹은 통계치

표본이 추출되어 통계량이 하나의 값으로 실현된 값이다. 즉 함수인 통계량에 관측값이 대입되어 나온 값이다. 주로 소문자로 $ \bar{x} $ , $ s^2 $ , $ \hat{p} $ 등과 같이 표기된다.

 

---

자료의 종류

 

• 양적 자료(Quantiative Data)와 질적 자료(Qualitative Data)

양적 자료는 관측 결과가 숫자로 표현되는 자료이다. 수치적 자료, 계량 자료라 말하기도 한다. 양적 자료는 다시 이산형 자료(discrete data)와 연속형 자료(continuous data)로 나눌 수 있다. 이산형 자료는 정수로 나타낼 수 있는, 예를 들어 자녀의 수, 교통사고 건수 등의 자료이고, 연속형 자료는 실수로 나타낼 수 있는, 예를 들어 키, 몸무게 등의 자료이다.

질적 자료는 관측 결과가 숫자가 아닌 범주나 속성으로 분류되는 자료이다. 범주형 자료, 비계량 자료라 말하기도 한다. 질적 자료는 다시 순위형 자료(ordinal data)와 명목형 자료(nominal data)로 나눌 수 있다. 순위형 자료는 말 그대로 순위가 있는 자료형으로 평점이나 석차, 선호도 등의 자료이며 부등식을 사용할 수 있는 자료이다. 명목형 자료는 자료의 특성만 알 수 있는 자료로 성별, 직업 등의 자료이다.

 

• 단변량 자료(Univariate Data)와 다변량 자료(Multivariate Data)

단변량 자료는 하나의 변수로 측정한 값으로 이루어진 자료이고, 다변량 자료는 둘 이상의 변수를 측정한 값으로 이루어진 자료이다.

 

• 횡단면 자료(Cross-Section Data)와 시계열 자료(Time-Series Data), 패널 자료(Panel Data)

횡단면 자료는 다수의 개체를 동일한 시점에서 관측하여 모든 자료로 예를 들어 2024년 9월 9일 장마감시 반도체 기업들의 주가는 횡단면 자료이다. 시계열 자료는 동일한 변수를 여러 다른 시점에서 반복적으로 관측하여 모든 자료로 예를 들어 삼성전자의 일별 주가는 시계열 자료이다. 패널 자료는 다수의 개체를 여러 시점에서 관측하여 모든 자료로 횡단면 자료가 시계열로 있는 자료라 생각하면 이해하기 쉽다. 예를 들어 반도체 기업들의 일별 주가를 생각하면 다수의 개체(반도체 기업들의 주가)를 여러 시점(일별)에서 관측하여 모든 자료기 때문에 패널 자료이다.

 

---

자료의 요약 및 표현

 

• 도수분포표 (Frequency Distribution Table)

구간	도수	상대도수	누적도수
10 - 14	1	0.067	1
15 - 19	3	0.200	4
20 - 24	4	0.267	8
25 - 29	5	0.267	12
30 - 34	3	0.200	15

도수분포표는 데이터를 구간(혹은 계급)으로 나누어 각 구간에 속하는 데이터 값의 빈도를 기록한 표이다. 이를 통해 데이터의 분포를 한눈에 파악할 수 있으며 데이터의 빈도와 패턴을 쉽게 분석할 수 있다. 도수분포표는 크게 구간, 도수, 상대도수, 누적도수로 구성될 수 있다.

구간은 데이터를 나누는 기준이고, 도수는 각 구간에 속하는 데이터 항목의 개수이다. 계급의 수 $ C $ 는 다음과 같이 계산할 수 있다.  $ C = 3.3 (\log_{10}^n)+1 $ . 여기서 $ n $ 은 자료의 수이다. 이 계산된 $ C $ 값은 일반적으로 가장 가까운 정수로 반올림한다. 계급의 간격 $ W $ 는 범위 $ R $ 을 계급의 수 $ C $ 로 나누어 계산한다. 이때 $ W $ 의 값은 역시 올림하여 정수로 만든다. 상대도수는 전체 데이터에서 각 구간의 도수가 차지하는 비율을 나타내고, 누적도수는 각 구간까지의 도수를 합한 값을 나타낸다.

도수분포표는 데이터의 분포를 시각적으로 쉽게 파악할 수 있고, 중앙 경향, 변동성, 데이터의 집중 정도를 파악하는데 용이하다는 점에서 장점이 있다. 그러나 본래 데이터 자체를 도수분포표를 통해 알 수 없다는 단점도 있다. 즉 도수분포표를 통해서는 직접적인 데이터의 평균, 분산 등을 계산할 수 없다.

 

• 줄기-잎 그림 (Stem-and-Leaf Plot)

줄기	잎
5 6 7 8 9	3        7        9        9 4        4        4        5        6        7        8 0        4        6        7        9 0        1        2        4        5        6        9 3        8

도수분포료로 데이터를 가공하면 본래 관측값이 사라지는 것, 즉 정보 손실이 일어나는데 줄기-잎 그림은 이것이 해결되어 본래 관측값이 남아있다. 줄기와 잎을 통해 본래 관측값을 모두 표현하는데, 따라서 관측값이 너무 많을 경우 줄기-잎 그림으로 나타내기 부적절하다. 또한 자료값이 흩어져 있더라도 줄기-잎 그림으로 나타내기 어렵다.

 

• 막대 그래프 (Bar Gragh)

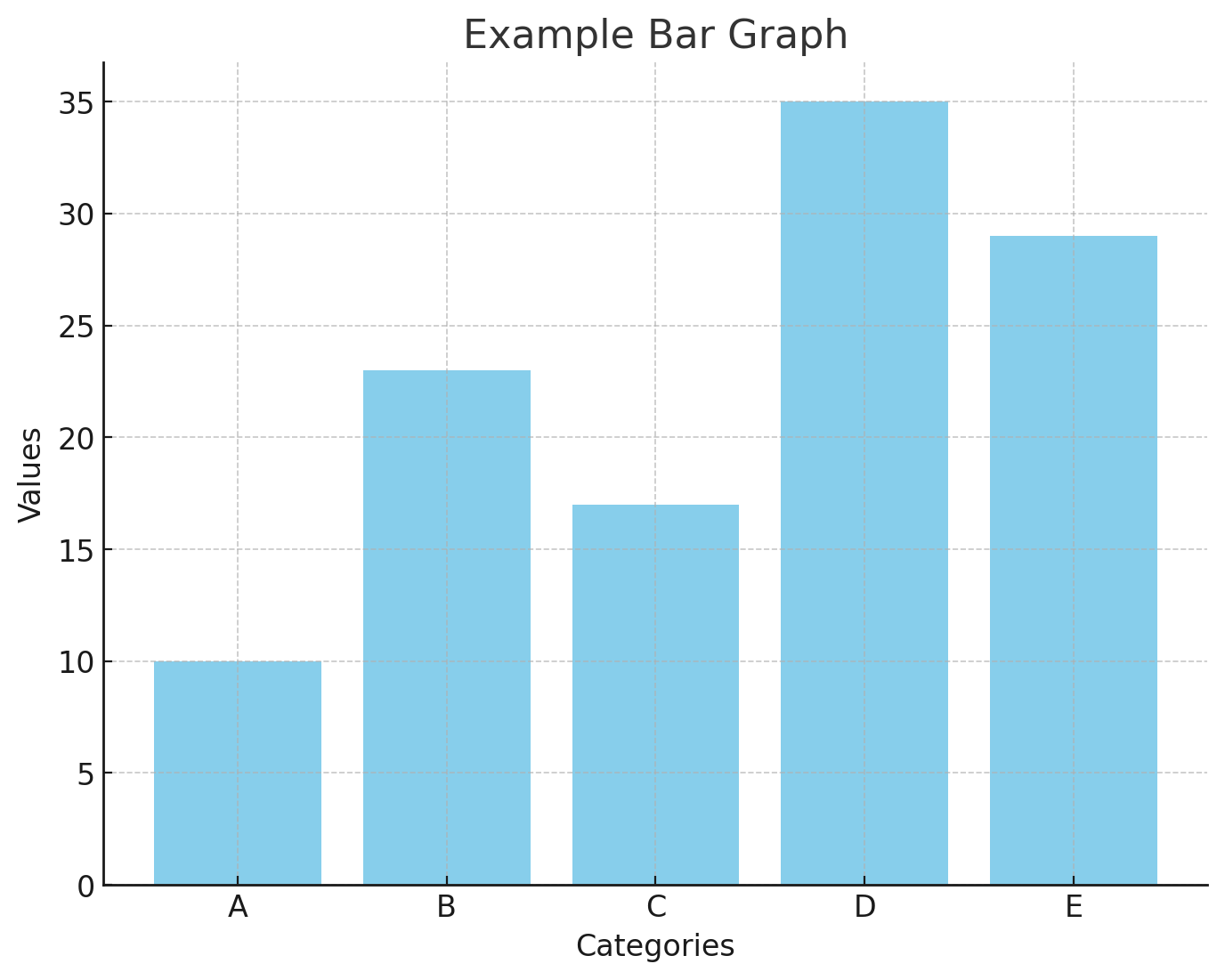
데이터를 막대로 표현한 그래프이다. 이산형, 명목형 자료에 많이 사용된다.

장점으로는 각 범주에 속하는 자료의 수나 비율을 쉽게 파악하여 비교가 용이하다는 점이 있다. 그러나 단점으로 각 범주가 전체에서 차지하는 비율 파악이 어렵고 범주나 많을 경우 막대 그래프로 나타내기 어렵다.

 

• 원 그래프 (Pie Chart)

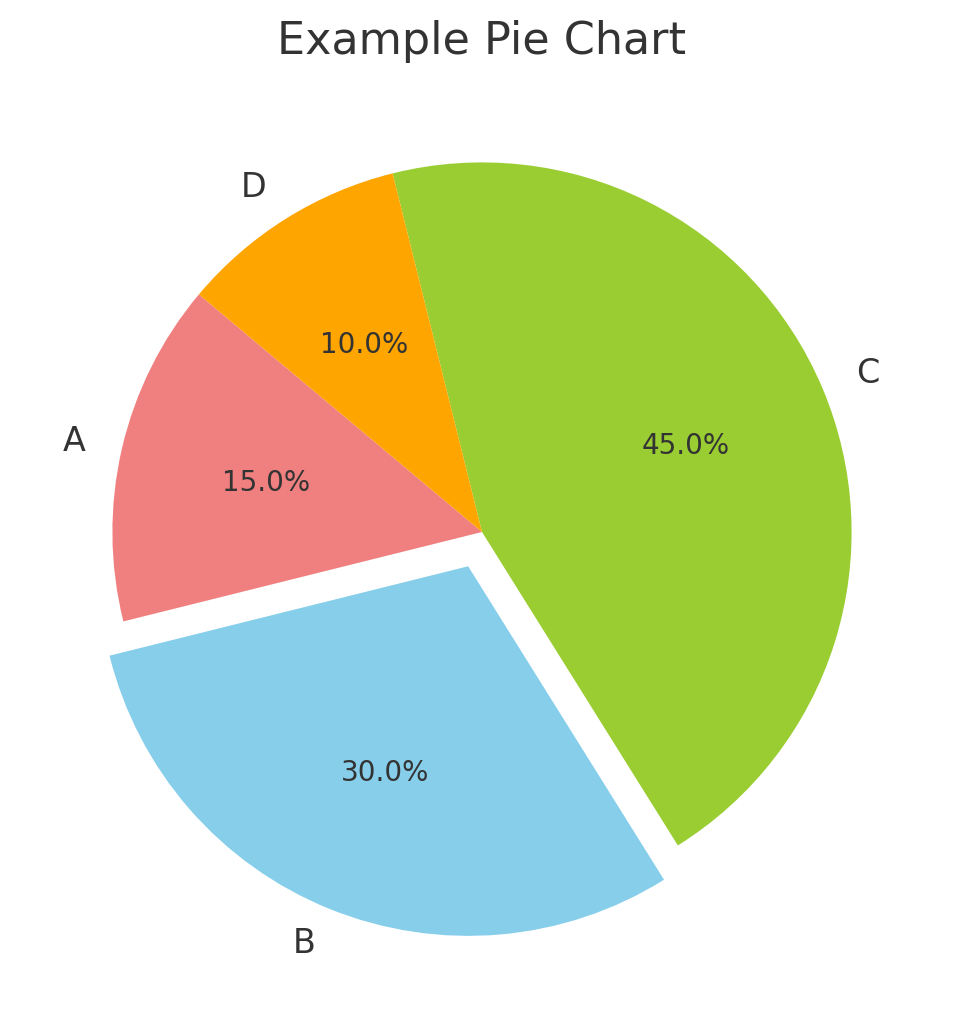
전체 중에서 각 부분이 차지하는 비율을 원 모양으로 시각화하는 그래프이다. 데이터의 비율을 직관적으로 보여줄 때 자주 사용된다.

단일 카테고리의 분포를 보여주기 적합하다는 장점이 있지만, 항목이 많아질 수록 해석이 어렵고, 비율 차이가 적을 경우에도 명확하게 확인하기 어렵다. 제약이 많기 때문에 잘 사용되지는 않는다.

 

• 히스토그램 (Histogram)

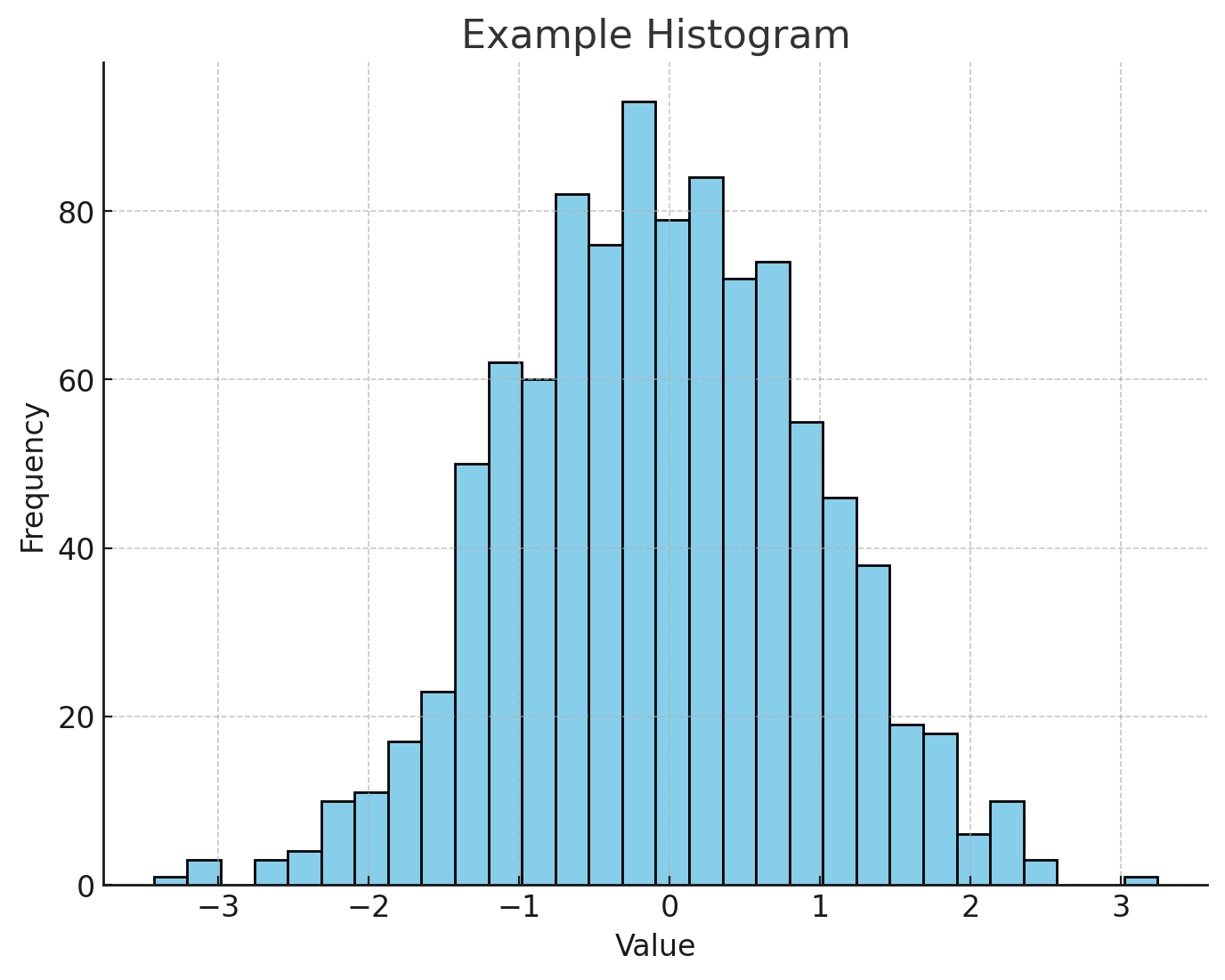
연속형 자료에 많이 사용되며 막대그래프와 구분하기 위해 막대 사이가 붙어 연속적으로 표현한다. 막대가 각 구간(bin)에 해당하는데 데이터를 구간으로 나눠서 데이터의 빈도를 막대의 높이로 표현한다. 이 구간의 개수를 적절하게 설정하는 것이 중요하다.

데이터의 분포를 쉽게 시각화하고, 데이터의 중앙 경향, 분산, 왜도 등을 파악하는 데에 유용하다. 그러나 범주형 데이터에는 적합하지 않고, 구간을 잘못 설정하면 데이터의 의미가 왜곡될 수 있다.

 

• 박스 플롯 (Box Plot)

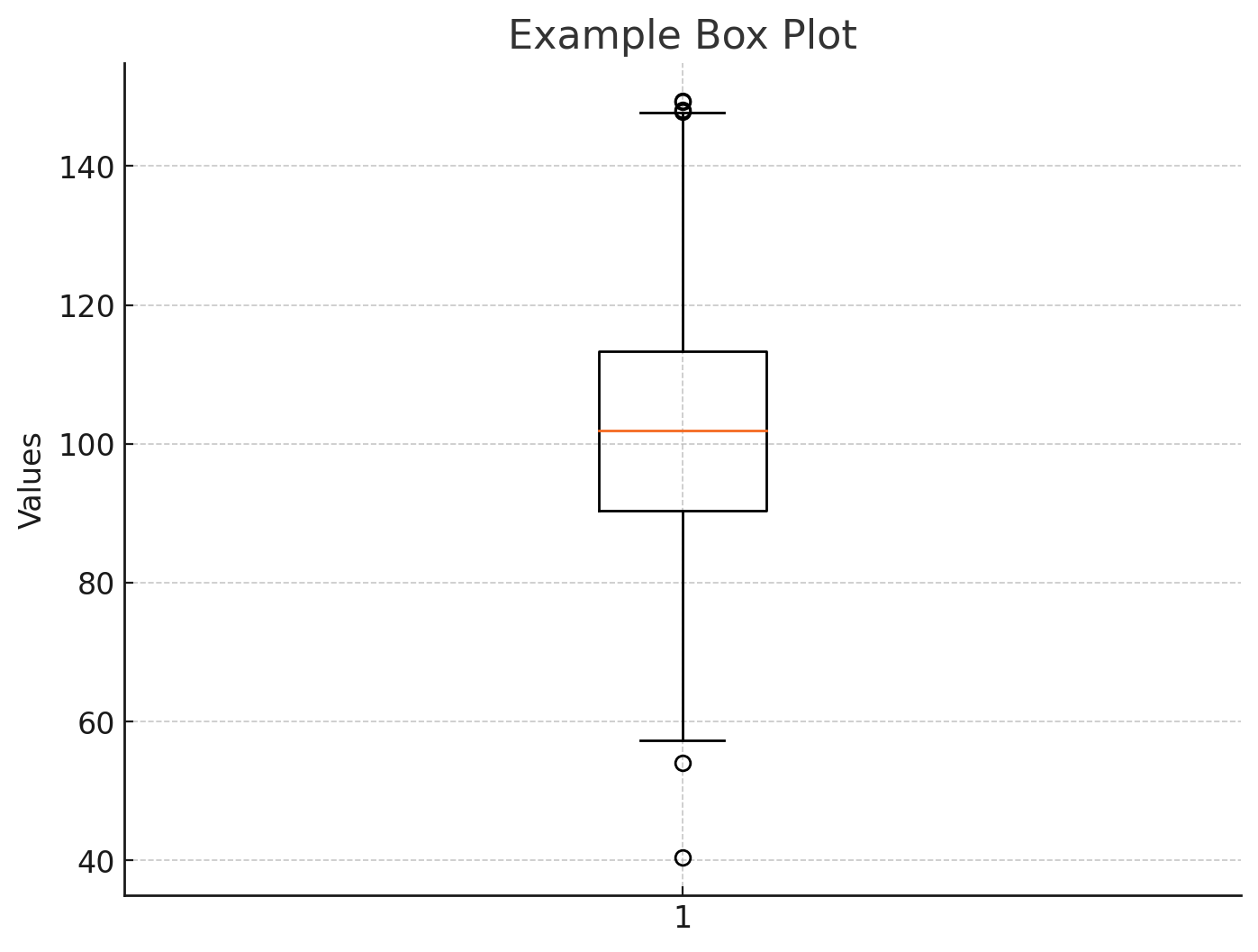
박스 플롯은 데이터의 분포와 요약 통계량을 시각적으로 표현하는 도구로, 특히 이상치를 쉽게 파악할 수 있다.

박스의 중앙 선은 데이터의 중앙값이고, 박스의 아래와 위쪽 경계는 1사분위수(Q1)와 3사분위수(Q3)이며, 따라서 박스는 데이터의 중간 50% 범위를 보여준다. 위아래로 뻗은 수염은 데이터의 유효한 최솟값과 최댓값을 나타내는데, 이 값들은 1사분위수(Q1)와 3사분위수(Q3)에서 IQR의 1.5배 이내에 있는 값 중에서 가장 작은 값과 가장 큰 값이다. IQR은 Q3 - Q1 에 해당한다. 수염 바깥 점으로 찍힌 데이터는 이상치로 간주된다.

데이터의 분포를 파악하는 데에 유용하고 이상치 데이터를 확인하기 쉽다는 장점이 있으나 데이터의 밀도 정보를 제공하지 못한다는 단점이 있다.

 

• 바이올린 플롯 (Violin Plot)

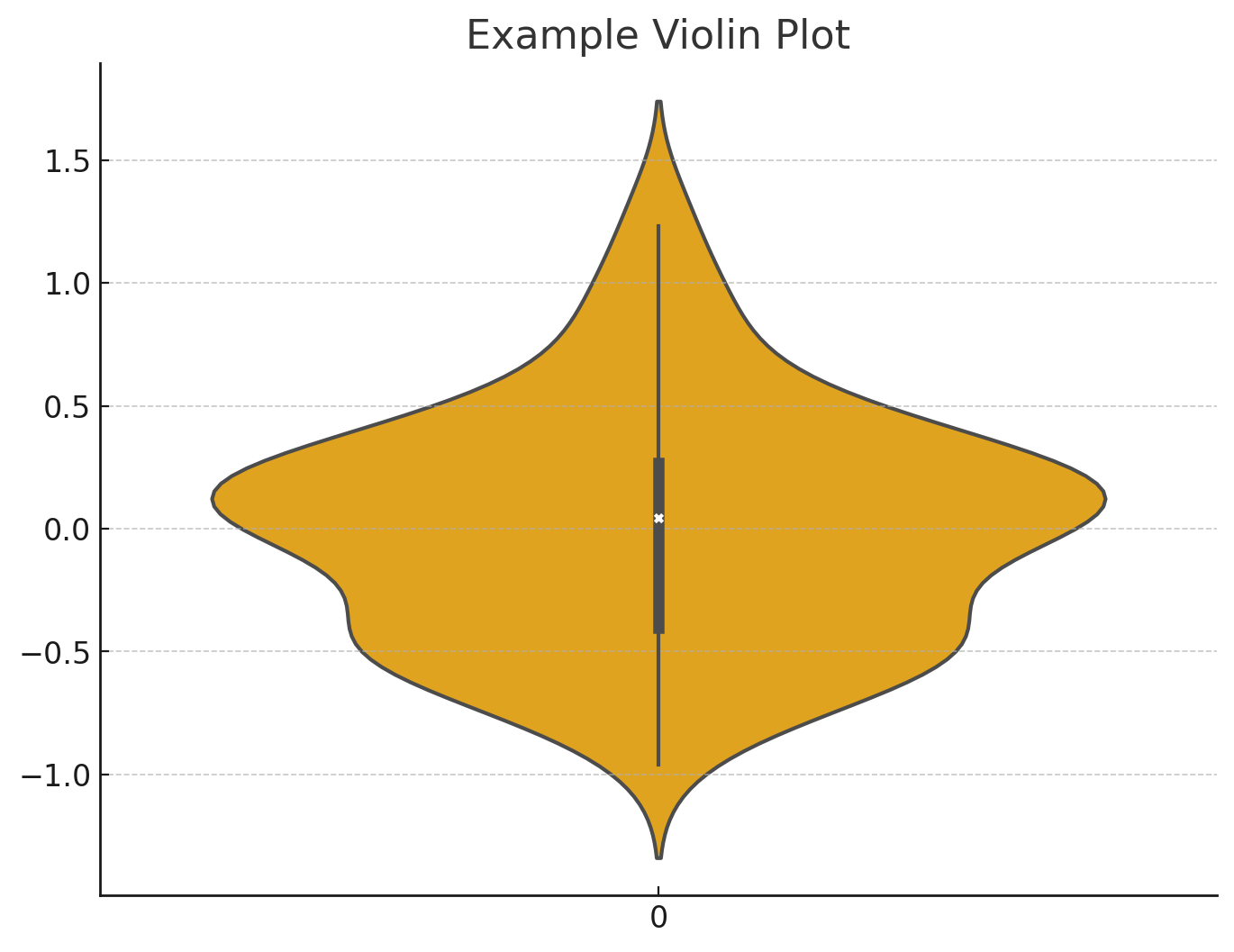
바이올린 플롯은 박스 플롯과 커널 밀도 추정(KDE)을 결합한 시각화 도구로 박스 플롯과 다르게 데이터의 밀도 정보도 제공하는 장점이 있다. 그러면서도 박스 플롯처럼 중앙값, 사분위수 역시 나타낸다.

좌우측으로 나타나는 곡선은 밀도 곡선으로 데이터의 밀도를 나타내는데, 곡선이 넓을수록 그 그간에 데이터가 더 많이 몰려있음을 의미한다. 히스토그램의 구간을 잘게 쪼개 옆으로 눕혀놨다고 생각하면 비슷하다. 단 데이터가 적을 경우 밀도 곡선이 정확한 분포를 반영하지 못할 수 있다.