[Descriptive Statistics] 왜도(skewness)와 첨도(kurtosis)

---

자료의 분포

 

위치측도, 중심위치측도, 산포측도는 대략적으로 자료의 대표적 성격을 보여준다. 그런데 단순히 이러한 측도들을 통해서는 자료의 비대칭성을 보일수는 없다. 자료의 분포가 좌우대칭이라는 전제가 있다면 평균과 분포만 있어도 대략적인 그림을 그릴 수 있겠지만, 그렇지 않다면 분포가 어느 방향으로 얼마나 기울어져 있는지 확인하고, 표현해야 자료의 특성을 정확히 표현할 수 있다.

 

---

왜도 (Skewness)

 

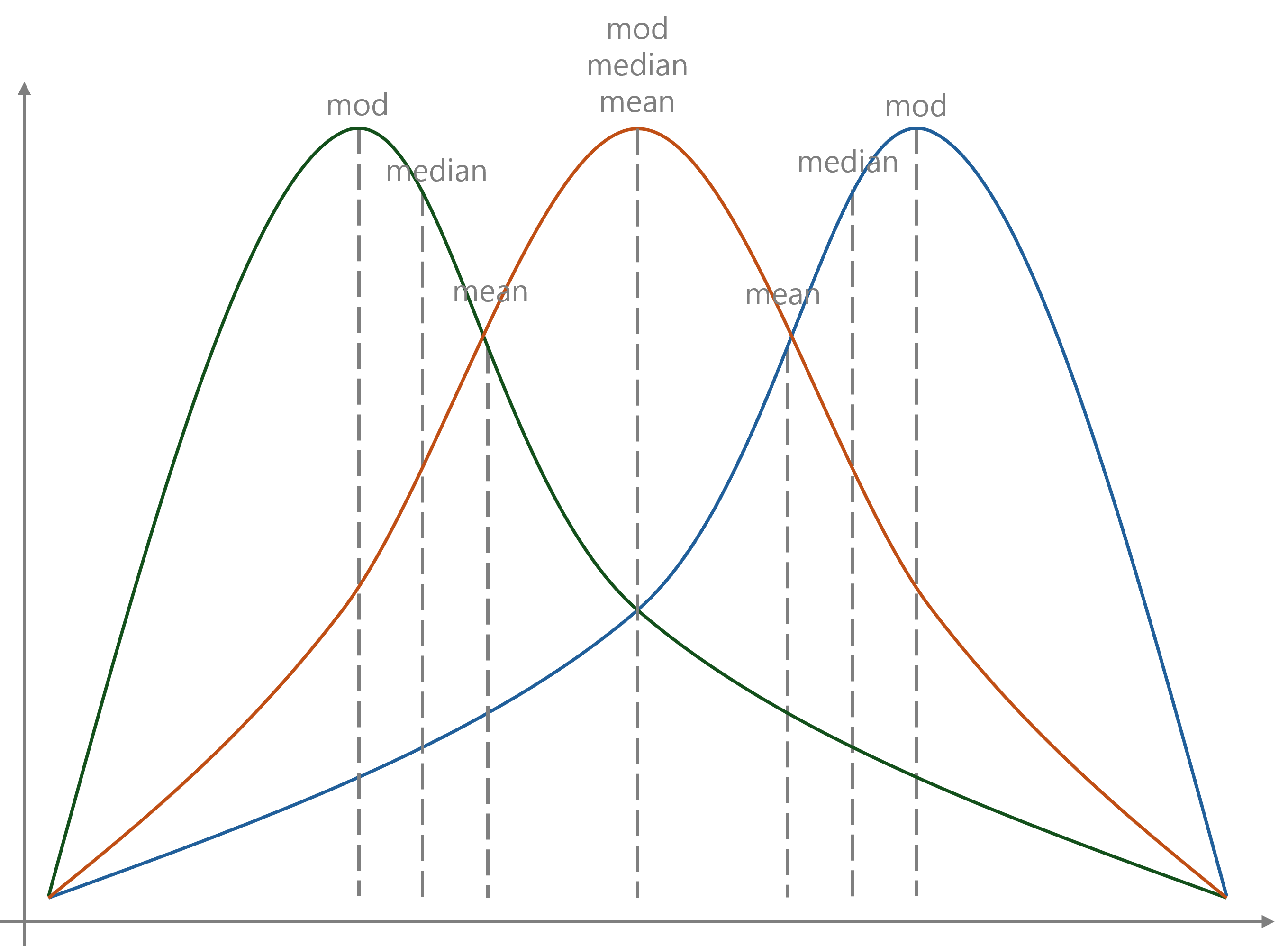
자료의 분포가 기울어진 정도를 의미한다. 왜도가 0 일 때 좌우대칭이며, 음수라면 오른쪽으로 긴 꼬리를 가진, 즉 왼쪽으로 치우쳐진 모양을, 양수라면 왼쪽으로 꼬리를 가진, 즉 오른쪽으로 치우쳐진 모양을 가진다. 왜도가 0 일 때가 위 그림에서 주황색, 음수일 때가 초록색, 양수일 때가 파란색 그래프이다.

분포가 기울어졌다는 것은 최빈값, 중앙값, 평균값이 다르다는 것을 말하기도 한다. 예를 들어 왜도가 양수인 파란색 그래프를 보면, 가장 높은 빈도를 말하는 최빈값, 즉 그래프에서 가장 높은 곳이 오른쪽으로 쏠려있다. 반면 중앙값은 그보다는 덜 오른쪽으로 쏠려있으며, 평균은 그보다 덜 쏠려있다. 즉 최빈값, 중앙값, 평균값의 차이를 통해서도 왜도를 유추할 수 있다. 최빈값이 평균값보다 크다면 왜도가 양수인 것이고, 반대로 평균값이 최빈값보다 크다면 왜도가 음수인 것이다.

 

---

첨도 (Kurtosis)

 

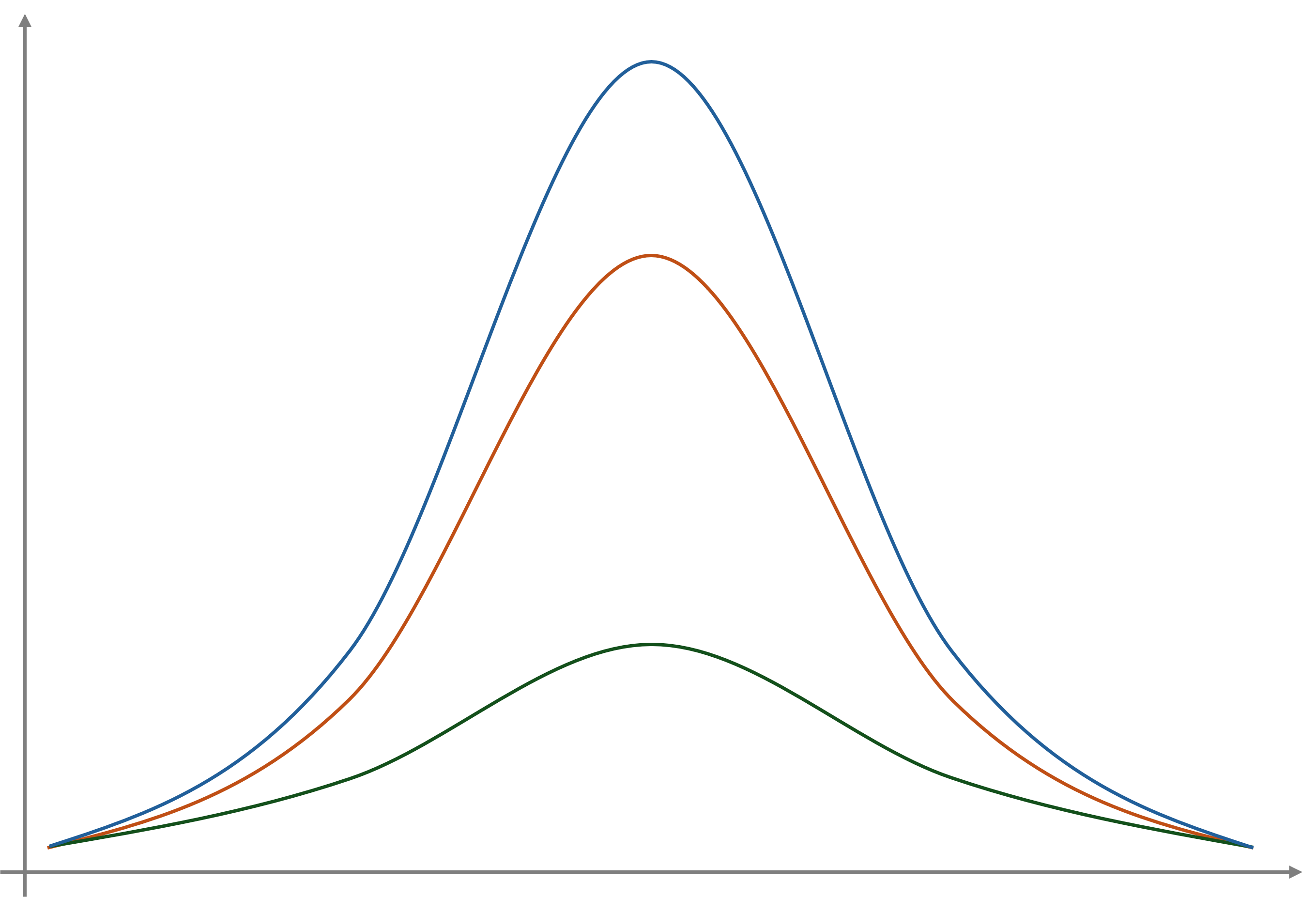
자료의 분포에서 꼬리의 두터움 정도를 나타낸다. 이상치가 많을수록, 즉 극단으로 값이 몰려 꼬리가 두꺼워질수록 큰 값을 띈다. 꼬리가 두꺼워지면 결과적으로 분포의 끝부분이 뾰족해지기 때문에 뾰족한 정도라고 오해하기도 한다. 위 그림에서는 파란색의 첨도가 가장 크고, 그 다음이 주황색, 그 다음 초록색 순으로 첨도가 크다.

일반적으로 첨도를 판단하는 기준은 정규분포인데, 정규분포의 첨도값이 3 이다보니 이를 0 으로 만들기 위해 3 을 뺀 첨도 값을 첨도값의 기준으로 삼는 경우도 있다. 이때의 첨도가 초과 첨도(excess kurtosis)이다.

자세한 왜도와 첨도는 적률(링크)에 대한 부분을 참고하여 확인하는 것이 좋다.