순차 탐색

말 그대로 순차적으로 탐색하는 방법이다. 주어진 리스트의 시작부터 끝까지 찾으려는 값인 탐색키와 비교하면서, 탐색키와 같으면 반환, 다르면 다음 값을 탐색한다. 정렬되지 않은 경우 최선의 방법일 수 있다.
값이 존재한다면 평균 비교 횟수는 $ (n+1) / 2 $ 이고, 값이 존재하지 않는다면 $ n $ 으로 시간복잡도는 $ \mathcal{O} (n) $ 이다.
조금 개선된 순환 탐색 방법으로는 탐색 대상 리스트의 끝에 탐색키를 삽입하고 탐색키와 같은 값을 찾을 때까지 탐색한 후 탐색된 값의 인덱스가 삽입한 리스트의 인덱스라면 탐색 실패로 처리하는 방법이 있다.
구현 | C
int sequential_search(int list[], int key, int low, int high) {
for(int i = low; i <= high; i++) {
if (list[i]==key) {
return i;
}
}
return -1;
}
색인 순차 탐색
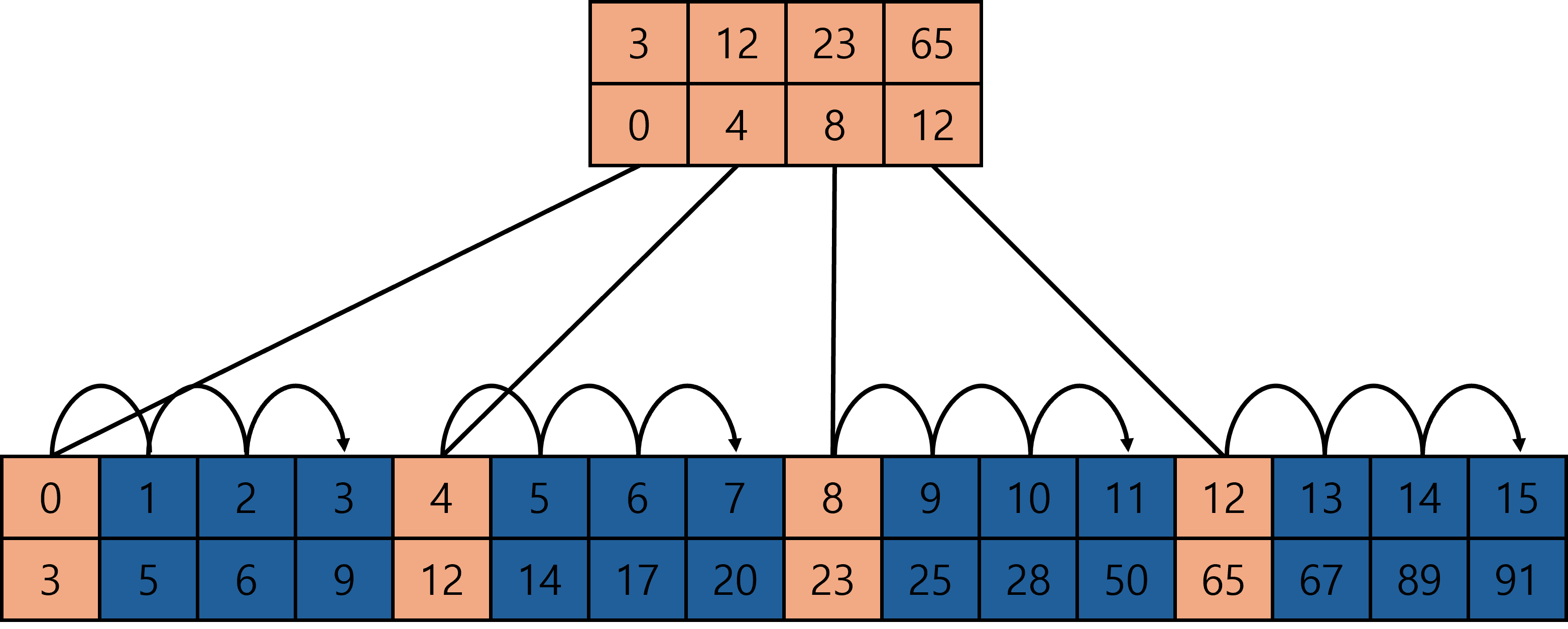
인덱스 테이블(index table)을 사용하여 탐색의 효율을 증대시키는 방법이다. 단 탐색 대상 리스트, 즉 주자료 테이블과 인덱스 테이블 모두 정렬되어 있어야 사용 가능한 방법이다.
인덱스 테이블에서 탐색키의 범위를 확인하고 주자료 테이블에서 해당 범위를 탐색한다. 따라서 시간복잡도는 평균적으로 $ \mathcal{O} (m + n/m) $ 이다. 이때 $ m $ 은 인덱스 테이블의 크기이다.
이진 탐색
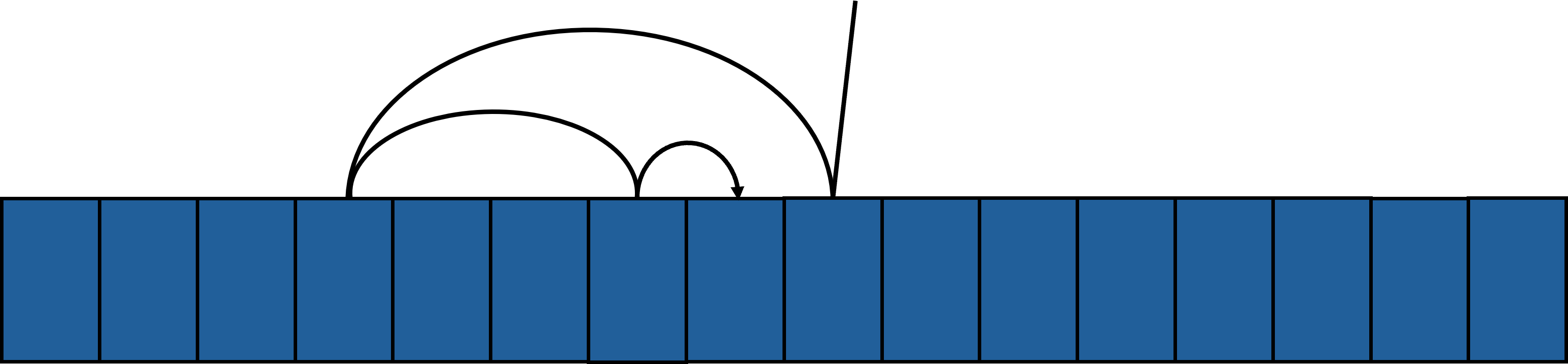
정렬된 리스트의 중앙에 있는 값을 확인하고, 탐색키와 비교하여 탐색키가 리스트의 어느 쪽에 있는지 확인하는 것으로 탐색 대상을 반씩 줄여나가며 탐색하는 방법이다. 단 정렬되어 있어야 한다는 조건이 있기 때문에 정렬되어 있지 않은 리스트에 대해서는 앞선 순차 탐색을 사용하는 것이 최선일 수 있다. 그러나 정렬되어 있는 리스트의 크기가 크다면 순차 탐색과는 비교도 안되게 효율적이다.
예를 들어 사전식으로 배열된 $10$억 개의 이름 리스트가 있다고 가정하자. 순차 탐색으로 이 리스트에서 특정 이름이 있는지 확인하고 싶다면 평균 $5$억번의 비교가 필요할 것이다. 그런데 이진 탐색으로 이 리스트에서 특정 이름이 있는지 확인하고 싶다면 대략 $30$번 내외로 찾을 수 있다. $ 2^{30} = 1073741824 $ 이기 때문이다.
시간복잡도는 균등 분할하여 값을 찾기 때문에 평균적인 경우 $ \mathcal{O} (\log_2 n) $ 이다.
구현 | C
int search_binary(int key, int low, int high) {
while(low <= high) {
int middle = (low+high)/2;
if (key == list[middle]) {
return middle;
}
else if (key > list[middle]) {
low = middle+1;
}
else {
high = middle-1;
}
}
return -1;
}
'Computer Science and Engineering > Data Structure' 카테고리의 다른 글
| [Data Structure] 균형 이진 탐색 트리(balanced binary search tree)와 AVL 트리 (0) | 2024.12.01 |
|---|---|
| [Data Structure] 보간 탐색(interpolation search) (0) | 2024.11.30 |
| [Data Structure] 기수 정렬(radix sort) 및 계수 정렬(counting sort) (0) | 2024.11.27 |
| [Data Structure] 병합 정렬(merge sort) (0) | 2024.11.27 |
| [Data Structure] 힙 정렬(heap sort) (0) | 2024.11.26 |
순차 탐색

말 그대로 순차적으로 탐색하는 방법이다. 주어진 리스트의 시작부터 끝까지 찾으려는 값인 탐색키와 비교하면서, 탐색키와 같으면 반환, 다르면 다음 값을 탐색한다. 정렬되지 않은 경우 최선의 방법일 수 있다.
값이 존재한다면 평균 비교 횟수는 (n+1)/2(n+1)/2 이고, 값이 존재하지 않는다면 nn 으로 시간복잡도는 O(n)O(n) 이다.
조금 개선된 순환 탐색 방법으로는 탐색 대상 리스트의 끝에 탐색키를 삽입하고 탐색키와 같은 값을 찾을 때까지 탐색한 후 탐색된 값의 인덱스가 삽입한 리스트의 인덱스라면 탐색 실패로 처리하는 방법이 있다.
구현 | C
int sequential_search(int list[], int key, int low, int high) {
for(int i = low; i <= high; i++) {
if (list[i]==key) {
return i;
}
}
return -1;
}
색인 순차 탐색

인덱스 테이블(index table)을 사용하여 탐색의 효율을 증대시키는 방법이다. 단 탐색 대상 리스트, 즉 주자료 테이블과 인덱스 테이블 모두 정렬되어 있어야 사용 가능한 방법이다.
인덱스 테이블에서 탐색키의 범위를 확인하고 주자료 테이블에서 해당 범위를 탐색한다. 따라서 시간복잡도는 평균적으로 O(m+n/m)O(m+n/m) 이다. 이때 mm 은 인덱스 테이블의 크기이다.
이진 탐색

정렬된 리스트의 중앙에 있는 값을 확인하고, 탐색키와 비교하여 탐색키가 리스트의 어느 쪽에 있는지 확인하는 것으로 탐색 대상을 반씩 줄여나가며 탐색하는 방법이다. 단 정렬되어 있어야 한다는 조건이 있기 때문에 정렬되어 있지 않은 리스트에 대해서는 앞선 순차 탐색을 사용하는 것이 최선일 수 있다. 그러나 정렬되어 있는 리스트의 크기가 크다면 순차 탐색과는 비교도 안되게 효율적이다.
예를 들어 사전식으로 배열된 1010억 개의 이름 리스트가 있다고 가정하자. 순차 탐색으로 이 리스트에서 특정 이름이 있는지 확인하고 싶다면 평균 55억번의 비교가 필요할 것이다. 그런데 이진 탐색으로 이 리스트에서 특정 이름이 있는지 확인하고 싶다면 대략 3030번 내외로 찾을 수 있다. 230=1073741824230=1073741824 이기 때문이다.
시간복잡도는 균등 분할하여 값을 찾기 때문에 평균적인 경우 O(log2n)O(log2n) 이다.
구현 | C
int search_binary(int key, int low, int high) {
while(low <= high) {
int middle = (low+high)/2;
if (key == list[middle]) {
return middle;
}
else if (key > list[middle]) {
low = middle+1;
}
else {
high = middle-1;
}
}
return -1;
}
'Computer Science and Engineering > Data Structure' 카테고리의 다른 글
| [Data Structure] 균형 이진 탐색 트리(balanced binary search tree)와 AVL 트리 (0) | 2024.12.01 |
|---|---|
| [Data Structure] 보간 탐색(interpolation search) (0) | 2024.11.30 |
| [Data Structure] 기수 정렬(radix sort) 및 계수 정렬(counting sort) (0) | 2024.11.27 |
| [Data Structure] 병합 정렬(merge sort) (0) | 2024.11.27 |
| [Data Structure] 힙 정렬(heap sort) (0) | 2024.11.26 |