보간 탐색
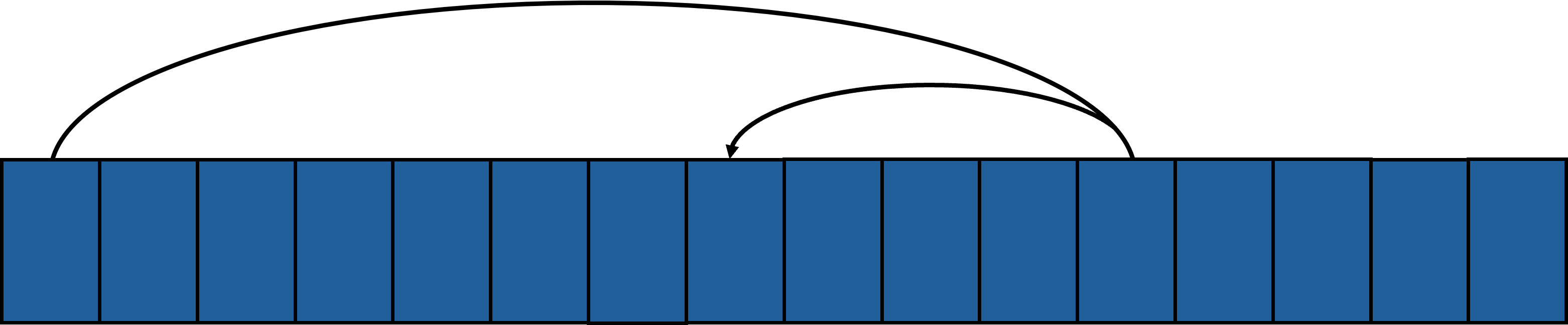
정렬된 리스트에서 탐색 범위를 줄여나가며 탐색하는 방식인데, 이진 탐색은 그냥 중앙을 탐색 위치로 지정하고 비교했다면 보간 탐색은 아래와 같은 공식을 이용해서 탐색 위치를 결정한다. 즉 이진 탐색이 균등 분할하였다면 보간 탐색은 불균등 분할하여 탐색한다.
$$ \dfrac{\text{key} - \text{list}[\text{low}]}{\text{list}[\text{high}] - \text{list}[\text{low}]} \times (\text{high} - \text{low}) + \text{low} $$
예를 들어 설명한다면 1400페이지의 전화번호부에서 하정우라는 이름을 찾는다고 해보자. 성에 ㅎ 이 들어가니까 당연히 중앙을 보는 것보다 1300페이지쯤부터 찾아보는 것이 효율적일 것이다. 이런식으로 정렬되어 있을 때 탐색키가 들어있을 곳을 추정하여 탐색 위치로 지정하는 것이 보간 탐색이다.
데이터가 균등하게 분포되어 있는 리스트에서는 굉장히 효율적이어서 평균적으로 $ \mathcal{O} (log_2(log_2 n)) $ 의 시간복잡도를 가지지만, 데이터가 불균등하게 분호되어 있는 리스트에서는 비효율적이어서 최악의 경우 $ \mathcal{O} (n) $ 의 시간복잡도는 가진다.
구현 | C
int interpol_search(int key, int n) {
int low = 0, high = n - 1;
while ((list[high] >= key) && (key > list[low])) {
int j = ((float)(key - list[low]) / (list[high] - list[low]) * (high - low)) + low;
if (key > list[j]) {
low = j + 1;
}
else if (key < list[j]) {
high = j - 1;
}
else {
low = j;
}
}
if (list[low] == key) {
return(low);
}
else {
return -1;
}
}
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] 2-3 트리(2-3 tree) (0) | 2024.12.01 |
|---|---|
| [Data Structure] 균형 이진 탐색 트리(balanced binary search tree)와 AVL 트리 (0) | 2024.12.01 |
| [Data Structure] 순차 탐색(sequential search), 색인 순차 탐색(indexed sequential search) 및 이진 탐색(binary search) (0) | 2024.11.30 |
| [Data Structure] 기수 정렬(radix sort) 및 계수 정렬(counting sort) (0) | 2024.11.27 |
| [Data Structure] 병합 정렬(merge sort) (0) | 2024.11.27 |