도구변수 (IV)
도구변수는 누락편의(참고링크), 측정오차(참고링크), 동시성(참고링크), 역인과성(참고링크) 등의 이유로 내생성(endogeneity) 문제가 발생해 OLS 추정치가 편향되는 상황을 해결하기 위해 사용한다. 내생성은 설명변수와 오차항이 상관되는 것을 말한다.
도구변수를 생각하기 위해 간단한 문제를 생각해보자. 과연 교육은 임금에 얼마나 많은 영향을 미칠까. 이를 회귀식으로 세운 것은 다음과 같다.
$$ Y_i = \alpha+ \beta S_i + \gamma A_i + \epsilon_i $$
여기서 $ Y_i $ 는 개인 $ i $ 의 임금의 로그를 씌운 값(log of earnings)이고, $ S_i $ 는 $ i $ 의 교육연수(shcooling), $ A_i $ 는 $ i $ 의 능력(individual ability)이다. 그런데 일반적으로 개인의 능력은 관찰 불가능하다.
그렇다면 개인의 능력을 생략하고 회귀식을 만들어 적합한다면 어떤 문제가 발생할까. 일단 여기서는 앞선 능력까지 반영한 회귀식이 $ Y_i $ 를 모두 설명할 수 있다고 가정하겠다. 즉 또 다른 혼동요인은 없다고 생각하자. 또한 $ \epsilon_i $ 는 모든 설명변수와 상관없는 회귀 잔차이다. 이때 개인의 능력을 생략한 회귀식은 다음과 같다.
$$ Y_i = \alpha + \beta S_i + \eta_i $$
여기서 $ \eta_i $ 는 다음과 같다.
$$ \eta_i = \gamma A_i + \epsilon_i $$
즉 오차항이 능력 $ A_i $ 까지 포함한다. 그런데 $ A_i $ 는 $ S_i $ 와 상관관계를 가지므로 결과적으로 $ S_i $ 는 $ \eta_i $ 와 상관되어 내생성 문제(endogeneity)가 발생한다.
최소제곱법으로 추정하여보면 문제를 확인할 수 있는데 $ \beta $ 를 추정해보면 다음과 같다.
$$ \hat{\beta }_{OLS} = \frac{\mathrm{Cov}(Y, S)}{\mathrm{Var}(S)} $$
이에 진짜 모형을 대입하자.
$$ \hat{\beta}_{OLS} = \frac{\mathrm{Cov}(\alpha + \beta S + \gamma A + \epsilon_i, S)}{\mathrm{Var}(S)} = \beta + \gamma \cdot \frac{\mathrm{Cov}(A, S)}{\mathrm{Var}(S)} $$
즉 $ \gamma \neq 0 $ 이라면 편향(bias)이 발생한다. 일반적으로 능력이 뛰어날 때 더 높은 임금을 받을 것으로 예상되기에 $ \gamma > 0 $ 이라 예상할 수 있고, 이는 $ \hat{\beta}_{OLS} > \beta $ 라는 것을 의미한다.
이를 조건에 맞는 도구변수를 도입함으로서 해결할 수 있다.
도구변수 $ Z_i $ 가 존재한다고 가정하자. 이 변수는 다음 두 조건을 만족해야 한다.
$$ \mathrm{Cov}(S, Z) \neq 0 $$
$$ \mathrm{Cov}(A, Z) = \mathrm{Cov}(\epsilon , Z) = 0 $$
여기서 $ Z $ 와 $ S $ 과 관련되어 있어야 하는 것을 도구 관련성(instrument relevance) 조건이라 하고, $ Z $ 는 오차항과 관련 없어야 하는 것을 도구 외생성(instrument exogeneity) 조건이라 한다. 도구 관련성은 통계적 검정이 가능하지만, 도구 외생성은 통계적 검정이 힘들다. 이는 뒤에서 다시 다루겠다.
그렇다면 두 조건을 만족하는 $ Z_i $ 를 도입하면 달라지는 점을 확인하자. 먼저 $ Y $ 와 $ Z $ 의 공분산을 확인하면 다음과 같다.
$$ \mathrm{Cov}(Y, Z) = \beta \mathrm{Cov}(S, Z) $$
$ \mathrm{Cov}(Y, Z) = \mathrm{Cov}(\alpha + \beta S + \gamma A + \epsilon_i, Z) $
$ = E[(\alpha + \beta S + \gamma A + \epsilon_i) \cdot Z] - E(\beta_0 + \beta S + \gamma A + \epsilon_i) E(Z) $
$ = \alpha E(Z) + \beta E(SZ) + \gamma E(AZ) + E(\epsilon_i Z) - \alpha E(Z) - \beta E(S)E(Z) - \gamma E(A)E(Z) - E(\epsilon_i )E(Z) $
$ = \beta \mathrm{Cov}(S, Z) + \gamma \mathrm{Cov}(A, Z) + \mathrm{Cov}(\epsilon_i , Z) $
$ = \beta \mathrm{Cov}(S, Z) $
그렇다면 이를 통해 추정한 $ \hat{\beta}_{IV} $ 는 다음과 같다.
$$ \hat{\beta}_{IV} = \frac{\mathrm{Cov}(Y, Z)}{\mathrm{Cov}(S, Z)} = \beta $$
표본에서는 다음과 같다.
$$ \hat{\beta}_{IV} = \frac{\sum_{i=1}^n (z_i - \bar{z})(y_i - \bar{y})}{\sum_{i=1}^n (z_i - \bar{z})(s_i - \bar{s})} $$
즉 적절한 도구변수를 선택할 수 있다면 $ \beta $ 에 대한 비편향 추정량을 얻을 수 있다.
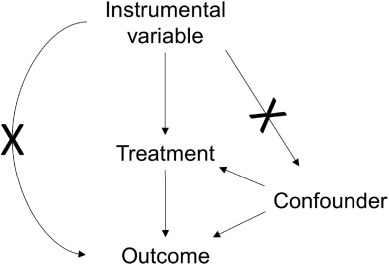
그림으로 보면 다음과 같다.
즉 혼동요인과 종속변수에는 영향을 주지 않는 도구변수를 통해 처치에만 관여하여 처치의 효과를 추정하는 것이다.
약한 도구변수 (Weak IV)
그러나 도구변수를 이용하는 방법에는 큰 문제가 있다. 앞서 언급한 바와 같이 도구변수는 도구 관련성(instrument relevance) 조건과 도구 외생성(instrument exogeneity) 조건을 모두 만족해야 한다. 그런데 누락변수와 도구변수의 관련성을 확인해야 알 수 있는 도구 외생성을 확인하기란 쉽지 않다. 아니 애초에 관련성을 확인할 수 있는 누락변수 데이터가 있었다면 굳이 도구변수를 사용하지 않아도 될 것이다. 즉 이는 가정으로 넘어가야 한다.
그런데 만약 외생성 조건이 만족하지 않는다면 어떻게 될까. 즉 다음과 같다고 해보자.
$$ Y_i = \alpha+ \beta S_i + \gamma A_i + \epsilon_i $$
$$ \mathrm{Cov}(A, Z) \neq 0, \quad \mathrm{Cov}(\epsilon , Z) \neq 0 $$
여기서 $ A $ 가 누락변수, $ Z $ 가 도구변수이다. 이때 다시 $ \beta $ 를 추정해보자.
$$ \hat{\beta}_{IV} = \frac{\mathrm{Cov}(Y, Z)}{\mathrm{Cov}(S, Z)} = \beta + \gamma \cdot \frac{\mathrm{Cov}(A,Z)}{\mathrm{Cov}(S,Z)} + \frac{\mathrm{Cov}(\epsilon,Z)}{\mathrm{Cov}(S,Z)} $$
원래는 외생성 조건으로 $ 0 $ 이 되어 불편성이 만족되어야 하지만 외생성 조건을 만족하지 않으면서 편향이 생겼다. 이를 다시 OLS로 추정해보자.
$$ \hat{\beta}_{OLS} = \beta + \gamma \cdot \frac{\mathrm{Cov}(A, S)}{\mathrm{Var}(S)} $$
이제 문제가 되는 부분을 확인할 수 있다. 도구변수를 이용한 추정은 OLS를 이용한 추정에서 생긴 편향을 제거하기 위한 방법이었는데, 계속 편향이 남게 되는 것이다.
또한 만약 도구변수와 설명변수의 상관관계가 약하다고 해보자. 즉 $ \mathrm{Cov}(S, Z) $ 가 작다고 해보자. 그렇다면 도구변수를 이용한 추정에서의 편향은 증가한다. 즉 다음과 같다.
$$ \mathrm{Cov}(S, Z) \downarrow \quad \Longrightarrow \quad \gamma \cdot \frac{\mathrm{Cov}(A,Z)}{\mathrm{Cov}(S,Z)} + \frac{\mathrm{Cov}(\epsilon,Z)}{\mathrm{Cov}(S,Z)} \uparrow \uparrow $$
좀 더 직관적인 비교를 위해 $ \gamma A_i + \epsilon_i = \eta_i $ 를 이용하자. 그렇다면 다음과 같다.
$$ \hat{\beta}_{IV} = \beta + \frac{\mathrm{corr}(Z, \eta)}{\mathrm{corr}(Z, S)} \cdot \frac{\sigma_\eta}{\sigma_S} $$
$$ \hat{\beta}_{OLS} = \beta + \mathrm{corr}(S, \eta) \cdot \frac{\sigma_\eta}{\sigma_S} $$
즉 $ \dfrac{\mathrm{corr}(Z, \eta)}{\mathrm{corr}(Z, S)} > \mathrm{corr}(S, \eta) $ 라면 도구변수를 이용하는 것이 OLS를 이용하는 추정보다 오히려 편향이 크다는 이야기이다.
'Economics > Causal Inference' 카테고리의 다른 글
| [Causal Inference] 비모수 추정(nonparametric estimation) (0) | 2025.04.20 |
|---|---|
| [Causal Inference] 2단계 최소제곱법(2SLS, two-stage least squares) (0) | 2025.04.09 |
| [Causal Inference] 동시성(simultaneity)과 역인과성(reverse cauality) (0) | 2025.04.09 |
| [Causal Inference] 측정오차(measurement error) (0) | 2025.04.09 |
| [Causal Inference] 누락 편의(omitted variable bias) (0) | 2025.04.01 |