타당성 검증
단순선형회귀모형은 세 가지 기본 전제가 필요했다. 먼저 독립변수 $ x $ 와 종속변수 $ y $ 간 선형 함수관계가 성립해야 했고, 오차항 $ \epsilon $ 은 서로 독립이며 $ N(0, \sigma^2) $ 을 따라야 했다.
그런데 이러한 기본 가정 자체에 대한 검증은 하지 않았기에, 즉 선형모델로 설명하기 적합한지에 대한 검증을 해야할 것이다. 이를 위해 적합결여검정(lack-of-fit test) 등을 활용한다.
적합결여검정 (Lack-of-Fit Test)
두 변수 $ x $ 와 $ y $ 사이의 함수관계가 다음과 같은 단순선형회귀모형으로 표현되는 것이 적합한지 알아보기 위해 적합결여검정을 진행한다.
$$ y = \beta_0 + \beta_1 x + \epsilon, \qquad ( \epsilon \sim N(0, \sigma^2) ) $$
이 검정은 $ x $ 의 각 수준(level)에서 반복측정(repeated observations) 값이 있어야만 가능하다.
$ x $ 의 수준으로 $ x_1, x_2, \cdots, x_k $ 가 있고, 각 수준에서 $n_1, n_2, \cdots, n_k $ 개의 반복된 관측값이 있다고 가정하자. 전체 자료의 수는 $ n = \sum_{i=1}^k n_i $ 으로 나타낸다. 이때 최소제곱법으로 구한 회귀모형을 다음과 같다 하자.
$$ \hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i , \qquad (i = 1, 2, \cdots, k) $$
하나의 $ x_i $ 에서는 $ n_i $ 개의 $ y $ 의 관측값이 있지만, 회귀모형으로 도출되는 $ y $ 의 추정값은 $ \hat{y}_i $ 하나 뿐이다. 이 경우 잔차 변동 $ SSE $ 는 다음과 같고, $ \bar{y}_i = \sum_{i=1}^{n_i} y_{ij} / n_i $ 를 이용해 분해할 수 있다.
$$ SSE = \sum_{i=1}^k \sum_{j=1}^{n_i} (y_{ij} - \hat{y}_i) ^2 $$
$$ = \sum_{i=1}^k \sum_{j=1}^{n_i} [(y_{ij} - \bar{y}_i)+(\bar{y}_i - \hat{y}_i)]^2 = \sum_{i=1}^k \sum_{j=1}^{n_i} (y_{ij} - \bar{y}_i)^2 + \sum_{i=1}^k n_i (\bar{y}_i - \hat{y}_i)^2 $$
분리된 식에서 첫번째 제곱합을 순오차제곱합(pure error sum of squares)라 한다.
$$ SSPE = \sum_{i=1}^k \sum_{j=1}^{n_i} (y_{ij} - \bar{y}_i)^2 $$
두번째 제곱합을 적합결여제곱합(lack-of-fit sum of squares)라 한다.
$$ SSLF = \sum_{i=1}^k n_i (\bar{y}_i - \hat{y}_i)^2 $$
이때 $ SSPE $ 관련 자유도는 $ n - k $ 이다. 따라서 순오차평균제곱(pure error mean square)은 다음과 같다.
$$ MSPE = \frac{SSPE}{n-k} $$
$ SSLF $ 관련 자유도는 $ k - 2 $ 이다. 따라서 적합결여평균제곱(lack-of-fit mean square)은 다음과 같다.
$$ MSLF = \frac{SSLF}{k-2} $$
그리고 회귀모형 $ E(Y \mid X = x) = \beta_0 + \beta_1 x $ 가 옳은가를 검정하기 위한 통계량 $ F_0 $ 는 다음과 같다.
$$ F_0 = \frac{MSLF}{MSPE} $$
추가적으로 회귀직선의 올바름과 관계없이 다음이 성립한다.
$$ E(MSPE) = \sigma^2 $$
$$ E(MSLF) = \sigma^2 + \frac{\sum_{i=1}^k n_i [E(y_i) - E(\hat{y}_i) ]^2}{k-2} $$
따라서 $ E(y_i) $ 와 $ E(\hat{y}_i) $ 가 가까울수록 $ F_0 $ 의 값은 $ 1 $ 에 가까워지고, 회귀직선모형이 옳은 가정이라는 뜻이 된다. 따라서 $ H_0 : E(Y \mid X=x) = \beta_0 + \beta_1 x $ 대 $ H_1 : E(Y \mid X=x) \neq \beta_0 + \beta_1 x $ 의 검정에서 유의수준 $ \alpha $ 에 대해 다음이 성립한다면 귀무가설을 기각한다.
$$ F_0 = \frac{MSLF}{MSPE} > F_{\alpha}(n-2, n-k) $$
잔차 검토
잔차는 $ e_i = y_i - \hat{y}_i = y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i $ 으로 정의하며, 그 합은 $ 0 $ 이다. 또한 각 잔차들이 i.i.d.라는 가정에 따라 각 잔차들을 이용하여 산점도를 그려본다면 평균인 $ 0 $ 을 중심으로 무작위해야 한다.
만약 무작위 하지 않다면, 다른 경우를 생각해보아야 한다.
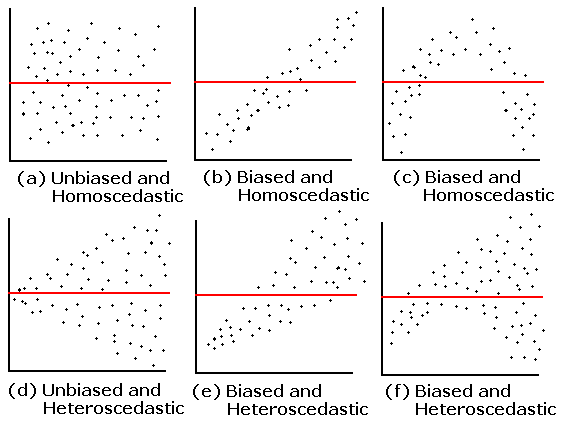
위 경우처럼 다양한 잔차의 패턴이 나올 수 있다. 가장 이상적인 것은 (a)로 평균을 중심으로 무작위 분산을 보인다. (b)와 (e)의 경우 어떤 선형항(linear term)이 추가되면 더 나을 것이라 보여준다. (c)와 (f)는 선형회귀로는 표현하기 어려워 보인다. (d)와 (e)는 잔차의 분산이커지는데 가중회귀모형을 이용하는 것이 적절할 수 있음을 보여준다.
참고로 잔차의 성질은 다음과 같다
$$ E(e_i) = 0 $$
$ E(e_i) = E(y_i) - E(\hat{y}_i) $
$ = (\beta_0 + \beta_1 x_i) - (\beta_0 + \beta_1 x_i) $
$ = 0$
$$ \mathrm{Var}(e_i) = \left[ 1 - \frac{1}{n} - \frac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \right] \cdot \sigma^2 $$
$ \mathrm{Var}(e_i) = \mathrm{Var}(y_i - \hat{y}_i) $
$ = \mathrm{Var}[ y_i - \bar{y} - \hat{\beta}_1 (x_i - \bar{x}) ] $
$ = \mathrm{Var}(y_i - \bar{y}) + (x_i + \bar{x}) \mathrm{Var}(\hat{\beta}_1) - 2 (x_i - \bar{x}) \mathrm{Cov} (y_i - \bar{y}, \hat{\beta}_1) $
이때 $ \mathrm{Cov} (y_i - \bar{y}, \hat{\beta}_1) = \dfrac{(x_i - \bar{x})}{\sum (x_i - \bar{x})^2} \sigma^2 $ 이다.
따라서 다음이 성립한다.
$ \left( 1 - \frac{1}{n} \right) \sigma^2 + \dfrac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \sigma^2 - 2 \dfrac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \sigma^2 $
$ = \left[ 1 - \frac{1}{n} - \dfrac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \right] \cdot \sigma^2 $
$$ \mathrm{Cov}(e_i, e_j) = - \left[ \frac{1}{n} + \frac{(x_i - \bar{x})(x_j - \bar{x})}{\sum_k (x_k - \bar{x})^2} \right] \cdot \sigma^2 $$