이변량 정규분포
이변량 정규분포는 두 확률변수의 분포가 정규분포를 따르는 확률분포로 다변량 정규분포의 특수한 형태이다.
확률변수 $ X_1, X_2 $ 가 각각 $ N(\mu_1, \sigma_1^2) $, $N(\mu_2, \sigma_2^2)$ 를 따르며 이변량 정규분포를 따른다면 이변량 밀도함수는 다음과 같다.
$$ f(x_1, x_2) = \dfrac{e^{-q(x_1, x_2)/2}}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho ^2 }} \qquad (-\infty < y_1, y_2 < \infty) $$
$$ q(x_1, x_2) = \dfrac{1}{1-\rho^2} \left[ \dfrac{(x_1 - \mu_1)^2}{\sigma_1^2} - 2 \rho \dfrac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 - \mu_2)^2}{\sigma_2^2} \right] $$
어떤 확률변수 $ X_1, X_2 $ 가 존재하고 두 확률변수의 결합확률밀도함수(joint PDF)가 $ f(x_1, x_2) $ 이고 $ X_1 = x_1 $ 이 주어질 때 $ X_2 $ 의 조건부분포에 대해 다음 가정이 가능하다 하자.
- $ f(x_2 \mid x_1) $ 은 정규확률밀도함수이다.
- $ E( X_2 \mid x_1) $ 은 $ x_1 $ 의 선형함수이다.
- $ V(X_2 \mid x_1) $ 은 $ x $ 값에 종속이지 않아 상수이다.
이때 $ E(X_1) = \mu_1 $, $ E(X_2) = \mu_2 $, $ V(X_1) = \sigma_1^2 $, $ V(X_2) = \sigma_2^2 $ 이라 하자.
$ E( X_2 \mid x_1) $ 은 $ x_1 $ 의 선형함수이기에 다음이 성립한다.
$ E(X_2 \mid x_1) = \mu_2 + \rho \frac{\sigma_2}{\sigma_1} ( x_1 - \sigma_1) $
$ V(X_2 \mid x_1) $ 은 $ x $ 값에 종속이지 않아 상수이기에 다음이 성립한다.
$ \sigma_{X_2 \mid x_1}^2 = E \left( \left[ X_2 - E ( X_2 \mid x_1 ) \right] ^2 \mid x_1 \right) = \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right]^2 f(x_2 \mid x_1) dx_2 $
양변에 $ F_{X_1}(x_1) $ 을 곱하고 $ x_1 $ 에 대해 적분하면 $ V(X_2 \mid x_1) $ 이 상수이므로 다음이 성립한다.
$ \int_{- \infty}^\infty \sigma_{X_2 \mid x_1} ^2 f_{X_1} dx_1 $ $ = \sigma_{X_2 \mid x_1}^2 \int_{- \infty}^\infty f_{X_1} dx_1 $ $ = \sigma_{X_2 \mid x_1}^2 $
$ = \int_{- \infty}^\infty \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2 f(x_2 \mid x_1) f_{X_1}(x_1) dx_2 dx_1 $
$ = \int_{- \infty}^\infty \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2 f(x_1 , x_2) dx_2 dx_1 $
$ = E \left[ (X_2 - \mu_2)^2 - 2 \rho \frac{\sigma_2}{\sigma_1} (X_1 - \mu_1) (X_2 - \mu_2) + \rho^2 \frac{\sigma_2^2}{\sigma_1^2} (X_1 - \mu_1)^2 \right] $
$ = E \left[ (X_2 -\mu_2)^2 \right] - 2 \rho \frac{\sigma_2}{\sigma_1} E \left[ (X_1 - \mu_1) (X_2 - \mu_2) \right] + \rho^2 \frac{\sigma_2^2}{\sigma_1^2} E \left[ (X_1 - \mu_1)^2 \right] $
$ = \sigma_2^2 - 2 \rho \frac{\sigma_2}{\sigma_1} \rho \sigma_1 \sigma_2 + \rho ^2 \frac{\sigma_2^2}{\sigma_1^2} $
$ = \sigma_2^2 ( 1 - \rho ^2) $
즉 $ \sigma_{X_2 \mid x_1}^2 = \sigma_2^2 ( 1 - \rho ^2) $ 이ek.
이떄 $ E(X_2 \mid x_1) $ 및 $ V(X_2 \mid x_1 ) $ 에 대한 가정은 $ f(x_2 \mid x_1) $ 은 정규확률밀도함수여야 하며 $ f(x_1 \mid x_1) $ 에 대해 다음이 성립해야 한다.
$$ f(x_2 \mid x_1) = \dfrac{1}{\sigma_2 \sqrt{2 \pi} \sqrt{1-\rho^2}} \exp \left( - \dfrac{\left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2}{2 \sigma_2^2 (1-\rho^2)} \right) \qquad ( -\infty < x_2 < \infty, \forall x_1 \in \mathbb{R} ) $$
그렇다면 이변량 밀도함수는 다음과 같다.
$ f(x_1, x_2) = f(x_2 \mid x_1) f_{X_1} (x_1) = \dfrac{e^{-q(x_1, x_2)/2}}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho ^2 }} \qquad (-\infty < y_1, y_2 < \infty) $
$ q(x_1, x_2) = \dfrac{1}{1-\rho^2} \left[ \dfrac{(x_1 - \mu_1)^2}{\sigma_1^2} - 2 \rho \dfrac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 - \mu_2)^2}{\sigma_2^2} \right] $
이러한 이변량 정규분포를 따르는 확률변수를 벡터와 행렬을 이용하여 다음과 같이 표현할 수 있다.
$$ \begin{bmatrix} X_1 \\ X_2 \end{bmatrix} \sim N \left( \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} , \begin{bmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{bmatrix} \right) $$
이때 $ \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} = \boldsymbol{\mu} $ 로 나타내고 평균벡터라 하며, $ \begin{bmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{bmatrix} = \mathbf{\Sigma} $ 로 나타내고 공분산 행렬이라 한다. 즉 $ X_1, X_2 $ 를 확률벡터 $ \mathbf{X} $ 로 묶으면 다음과 같이 나타낼 수 있다.
$$ \mathbf{X} \sim N (\boldsymbol{\mu}, \mathbf{\Sigma}) $$
참고로 $ \rho $ 가 상관계수이기 때문에 $ \rho \sigma_1 \sigma_2 = \operatorname{Cov} (X_1, X_2) $ 이다.
상관관계
만약 확률변수 $ X $ 와 $ Y $ 가 상관계수가 $ \rho $ 인 이변량 정규분포를 따르면 $ X$ 와 $ Y $ 가 독립이기 위한 필요충분조건은 $ \rho = 0 $ 이다.
참고로 앞서 언급했듯이 $ \rho \sigma_X \sigma_Y = \operatorname{Cov} (X, Y) $ 이다. 즉 $ \sigma_X , \sigma_Y > 0 $ 이란 조건아래 $ \operatorname{Cov} (X, Y) = 0 $ 이 $ X $ 와 $ Y $ 가 독립이기 위한 필요충분조건인 것이다.
단 항상 두 확률변수의 공분산이 $0$ 이라는 사실이 두 확률변수가 독립이기 위한 필요충분조건은 아니다. 이변량 정규분포를 따르는 경우에 두 확률변수의 공분산이 $0$ 일 때 두 확률변수가 독립인 것이다.
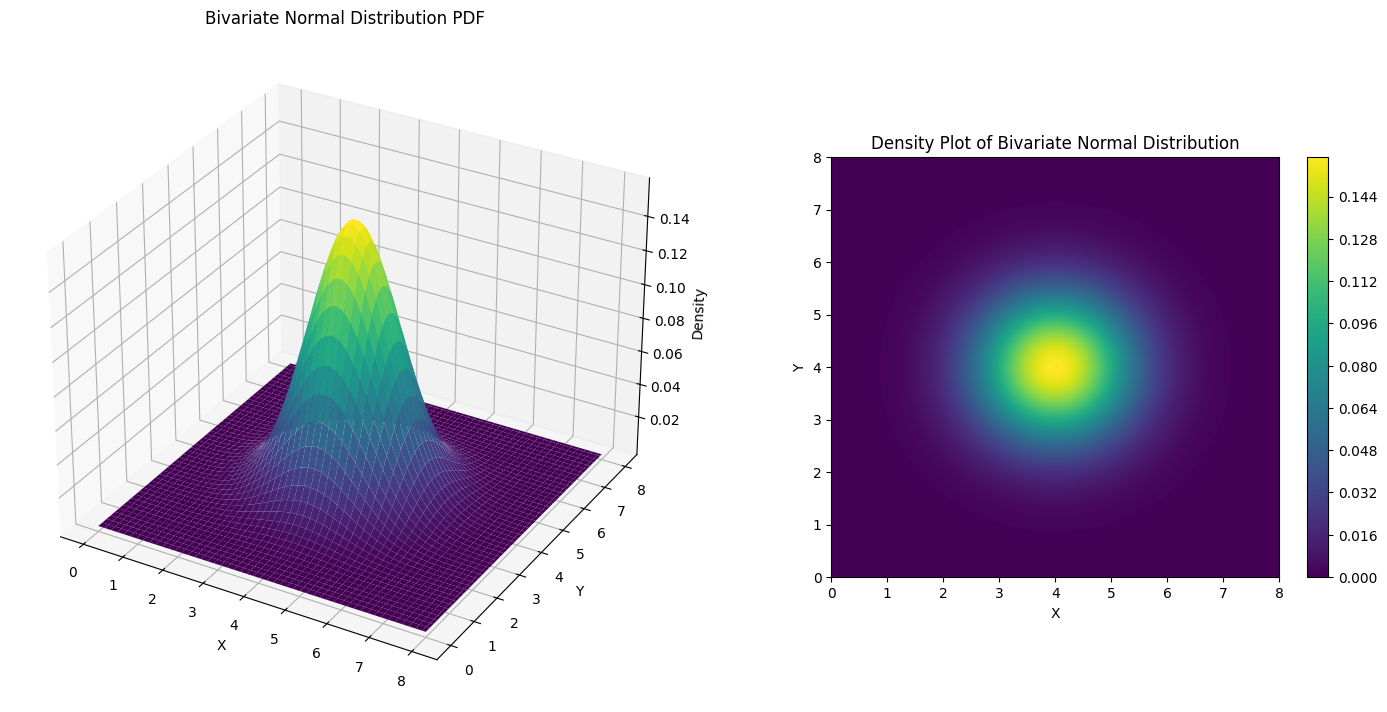
이러한 분포의 PDF를 그려볼 수 있을텐데 $ X $ 와 $ Y $ 의 각 평균이 $ 4 $, 분산이 $ 1 $ 인 경우라면 아래와 같이 그려볼 수 있다.
$ \rho = 0 $ 인 경우는 아래와 같다.
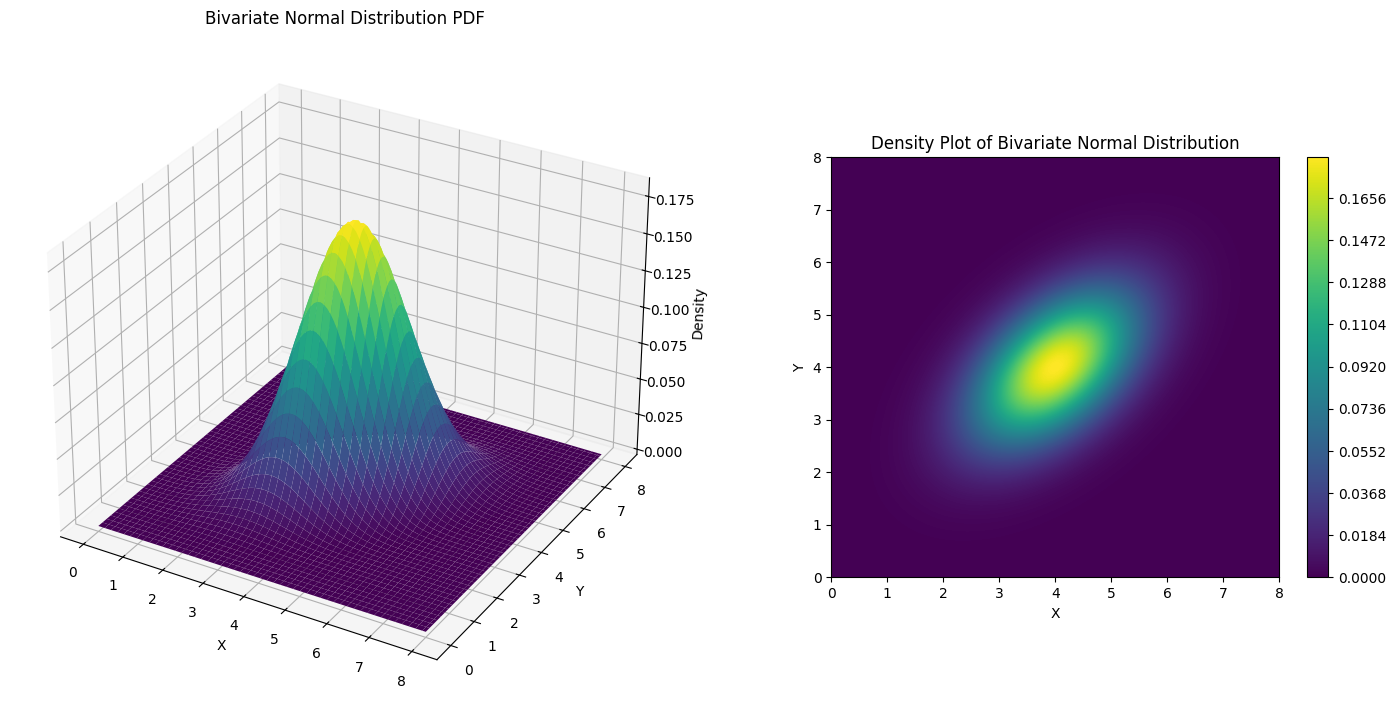
$ \rho = 0.5 $ 인 경우는 아래와 같다.
$ \rho = -0.5 $ 인 경우는 아래와 같다.
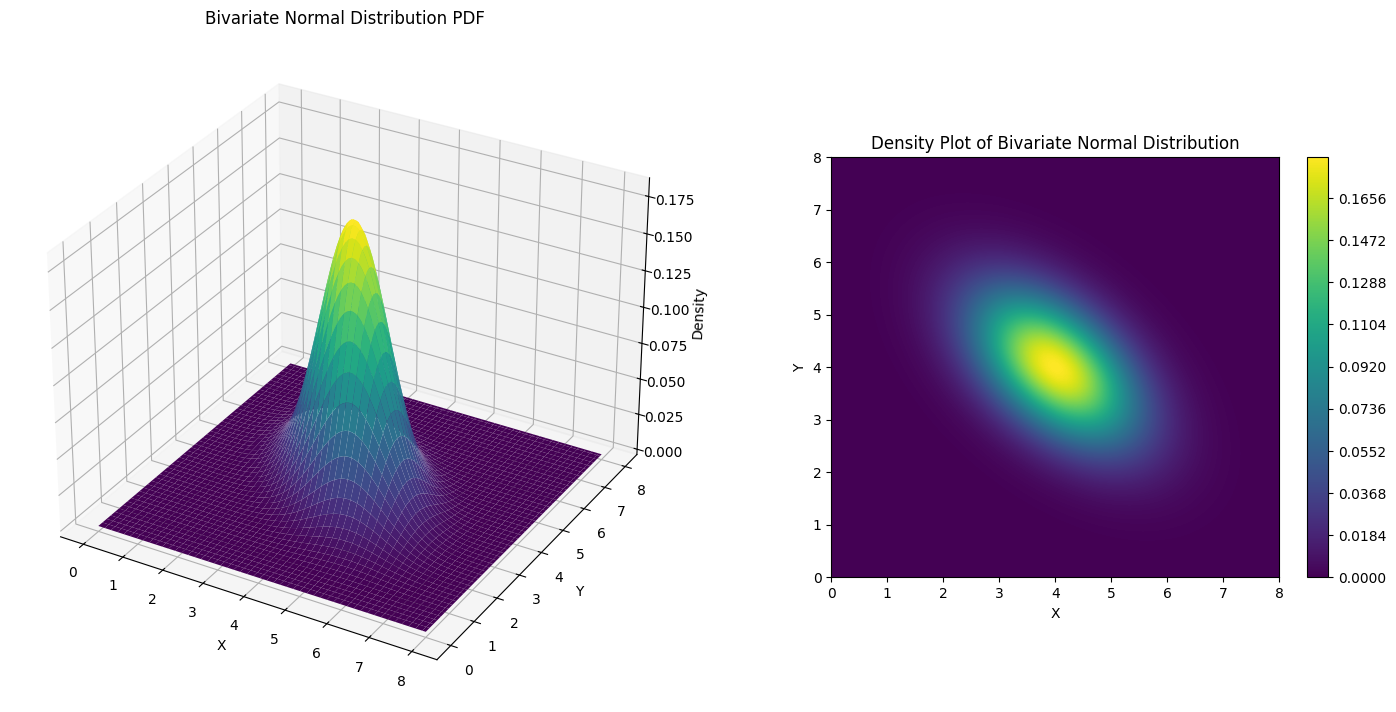
$ XY $ 축 좌표를 기준으로 양의 상관관계를 가지면 상승, 음의 상관관계를 가지면 하강하는 모습의 등고선이 나오는 것을 확인할 수 있다.
주변분포
확률변수 $ X $ 와 $ Y $ 가 이변량 정규분포를 따르면 주변분포는 어쩌면 당연하게도 각 $ X $ 와 $ Y $ 의 분포이다. 즉 각 확률변수의 주변확률밀도함수는 아래와 같다.
$$ f_X(x) = \dfrac{1}{\sqrt{2 \pi \sigma_X^2}} \exp \left( - \dfrac{(x-\mu_X)^2}{2 \sigma_X^2} \right) $$
$$ f_Y(y) = \dfrac{1}{\sqrt{2 \pi \sigma_Y^2}} \exp \left( - \dfrac{(y-\mu_Y)^2}{2 \sigma_Y^2} \right) $$
'Statistics > Mathematical Statistics' 카테고리의 다른 글
이변량 정규분포
이변량 정규분포는 두 확률변수의 분포가 정규분포를 따르는 확률분포로 다변량 정규분포의 특수한 형태이다.
확률변수 $ X_1, X_2 $ 가 각각 $ N(\mu_1, \sigma_1^2) $, $N(\mu_2, \sigma_2^2)$ 를 따르며 이변량 정규분포를 따른다면 이변량 밀도함수는 다음과 같다.
$$ f(x_1, x_2) = \dfrac{e^{-q(x_1, x_2)/2}}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho ^2 }} \qquad (-\infty < y_1, y_2 < \infty) $$
$$ q(x_1, x_2) = \dfrac{1}{1-\rho^2} \left[ \dfrac{(x_1 - \mu_1)^2}{\sigma_1^2} - 2 \rho \dfrac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 - \mu_2)^2}{\sigma_2^2} \right] $$
어떤 확률변수 $ X_1, X_2 $ 가 존재하고 두 확률변수의 결합확률밀도함수(joint PDF)가 $ f(x_1, x_2) $ 이고 $ X_1 = x_1 $ 이 주어질 때 $ X_2 $ 의 조건부분포에 대해 다음 가정이 가능하다 하자.
- $ f(x_2 \mid x_1) $ 은 정규확률밀도함수이다.
- $ E( X_2 \mid x_1) $ 은 $ x_1 $ 의 선형함수이다.
- $ V(X_2 \mid x_1) $ 은 $ x $ 값에 종속이지 않아 상수이다.
이때 $ E(X_1) = \mu_1 $, $ E(X_2) = \mu_2 $, $ V(X_1) = \sigma_1^2 $, $ V(X_2) = \sigma_2^2 $ 이라 하자.
$ E( X_2 \mid x_1) $ 은 $ x_1 $ 의 선형함수이기에 다음이 성립한다.
$ E(X_2 \mid x_1) = \mu_2 + \rho \frac{\sigma_2}{\sigma_1} ( x_1 - \sigma_1) $
$ V(X_2 \mid x_1) $ 은 $ x $ 값에 종속이지 않아 상수이기에 다음이 성립한다.
$ \sigma_{X_2 \mid x_1}^2 = E \left( \left[ X_2 - E ( X_2 \mid x_1 ) \right] ^2 \mid x_1 \right) = \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right]^2 f(x_2 \mid x_1) dx_2 $
양변에 $ F_{X_1}(x_1) $ 을 곱하고 $ x_1 $ 에 대해 적분하면 $ V(X_2 \mid x_1) $ 이 상수이므로 다음이 성립한다.
$ \int_{- \infty}^\infty \sigma_{X_2 \mid x_1} ^2 f_{X_1} dx_1 $ $ = \sigma_{X_2 \mid x_1}^2 \int_{- \infty}^\infty f_{X_1} dx_1 $ $ = \sigma_{X_2 \mid x_1}^2 $
$ = \int_{- \infty}^\infty \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2 f(x_2 \mid x_1) f_{X_1}(x_1) dx_2 dx_1 $
$ = \int_{- \infty}^\infty \int_{- \infty}^\infty \left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2 f(x_1 , x_2) dx_2 dx_1 $
$ = E \left[ (X_2 - \mu_2)^2 - 2 \rho \frac{\sigma_2}{\sigma_1} (X_1 - \mu_1) (X_2 - \mu_2) + \rho^2 \frac{\sigma_2^2}{\sigma_1^2} (X_1 - \mu_1)^2 \right] $
$ = E \left[ (X_2 -\mu_2)^2 \right] - 2 \rho \frac{\sigma_2}{\sigma_1} E \left[ (X_1 - \mu_1) (X_2 - \mu_2) \right] + \rho^2 \frac{\sigma_2^2}{\sigma_1^2} E \left[ (X_1 - \mu_1)^2 \right] $
$ = \sigma_2^2 - 2 \rho \frac{\sigma_2}{\sigma_1} \rho \sigma_1 \sigma_2 + \rho ^2 \frac{\sigma_2^2}{\sigma_1^2} $
$ = \sigma_2^2 ( 1 - \rho ^2) $
즉 $ \sigma_{X_2 \mid x_1}^2 = \sigma_2^2 ( 1 - \rho ^2) $ 이ek.
이떄 $ E(X_2 \mid x_1) $ 및 $ V(X_2 \mid x_1 ) $ 에 대한 가정은 $ f(x_2 \mid x_1) $ 은 정규확률밀도함수여야 하며 $ f(x_1 \mid x_1) $ 에 대해 다음이 성립해야 한다.
$$ f(x_2 \mid x_1) = \dfrac{1}{\sigma_2 \sqrt{2 \pi} \sqrt{1-\rho^2}} \exp \left( - \dfrac{\left[ x_2 - \mu_2 - \rho \frac{\sigma_2}{\sigma_1}(x_1 - \mu_1) \right] ^2}{2 \sigma_2^2 (1-\rho^2)} \right) \qquad ( -\infty < x_2 < \infty, \forall x_1 \in \mathbb{R} ) $$
그렇다면 이변량 밀도함수는 다음과 같다.
$ f(x_1, x_2) = f(x_2 \mid x_1) f_{X_1} (x_1) = \dfrac{e^{-q(x_1, x_2)/2}}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho ^2 }} \qquad (-\infty < y_1, y_2 < \infty) $
$ q(x_1, x_2) = \dfrac{1}{1-\rho^2} \left[ \dfrac{(x_1 - \mu_1)^2}{\sigma_1^2} - 2 \rho \dfrac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \dfrac{(x_2 - \mu_2)^2}{\sigma_2^2} \right] $
이러한 이변량 정규분포를 따르는 확률변수를 벡터와 행렬을 이용하여 다음과 같이 표현할 수 있다.
$$ \begin{bmatrix} X_1 \\ X_2 \end{bmatrix} \sim N \left( \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} , \begin{bmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{bmatrix} \right) $$
이때 $ \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} = \boldsymbol{\mu} $ 로 나타내고 평균벡터라 하며, $ \begin{bmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{bmatrix} = \mathbf{\Sigma} $ 로 나타내고 공분산 행렬이라 한다. 즉 $ X_1, X_2 $ 를 확률벡터 $ \mathbf{X} $ 로 묶으면 다음과 같이 나타낼 수 있다.
$$ \mathbf{X} \sim N (\boldsymbol{\mu}, \mathbf{\Sigma}) $$
참고로 $ \rho $ 가 상관계수이기 때문에 $ \rho \sigma_1 \sigma_2 = \operatorname{Cov} (X_1, X_2) $ 이다.
상관관계
만약 확률변수 $ X $ 와 $ Y $ 가 상관계수가 $ \rho $ 인 이변량 정규분포를 따르면 $ X$ 와 $ Y $ 가 독립이기 위한 필요충분조건은 $ \rho = 0 $ 이다.
참고로 앞서 언급했듯이 $ \rho \sigma_X \sigma_Y = \operatorname{Cov} (X, Y) $ 이다. 즉 $ \sigma_X , \sigma_Y > 0 $ 이란 조건아래 $ \operatorname{Cov} (X, Y) = 0 $ 이 $ X $ 와 $ Y $ 가 독립이기 위한 필요충분조건인 것이다.
단 항상 두 확률변수의 공분산이 $0$ 이라는 사실이 두 확률변수가 독립이기 위한 필요충분조건은 아니다. 이변량 정규분포를 따르는 경우에 두 확률변수의 공분산이 $0$ 일 때 두 확률변수가 독립인 것이다.
이러한 분포의 PDF를 그려볼 수 있을텐데 $ X $ 와 $ Y $ 의 각 평균이 $ 4 $, 분산이 $ 1 $ 인 경우라면 아래와 같이 그려볼 수 있다.
$ \rho = 0 $ 인 경우는 아래와 같다.

$ \rho = 0.5 $ 인 경우는 아래와 같다.

$ \rho = -0.5 $ 인 경우는 아래와 같다.

$ XY $ 축 좌표를 기준으로 양의 상관관계를 가지면 상승, 음의 상관관계를 가지면 하강하는 모습의 등고선이 나오는 것을 확인할 수 있다.
주변분포
확률변수 $ X $ 와 $ Y $ 가 이변량 정규분포를 따르면 주변분포는 어쩌면 당연하게도 각 $ X $ 와 $ Y $ 의 분포이다. 즉 각 확률변수의 주변확률밀도함수는 아래와 같다.
$$ f_X(x) = \dfrac{1}{\sqrt{2 \pi \sigma_X^2}} \exp \left( - \dfrac{(x-\mu_X)^2}{2 \sigma_X^2} \right) $$
$$ f_Y(y) = \dfrac{1}{\sqrt{2 \pi \sigma_Y^2}} \exp \left( - \dfrac{(y-\mu_Y)^2}{2 \sigma_Y^2} \right) $$