시그모이드 함수 (Sigmoid Function)
$$ y = \frac{1}{1 + e^{-x}} $$
시그모이드 함수는 위와 같은데, 그림으로 그려보면 아래와 같다.
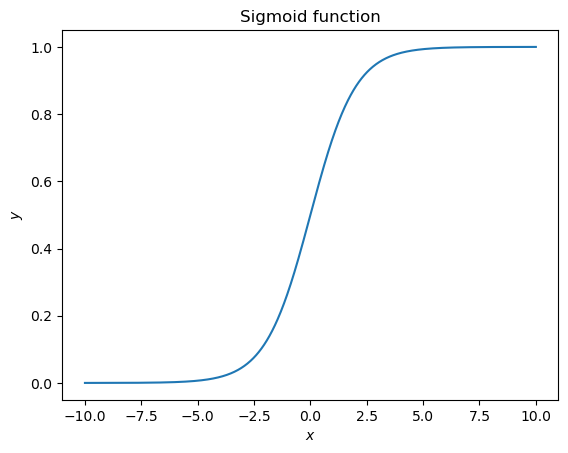
즉 $ (0, 0.5) $ 를 기준으로 점대칭이고, $ x $ 가 커지면 $ 1 $ 로, 작아지면 $ 0 $ 으로 수렴한다.
시그모이드 함수를 $ x $ 에 대해 미분하면 다음과 같다.
$$ \frac{\partial y}{\partial x} = y ( 1 - y) $$
시그모이드 함수 자체는 성공 확률과 실패 확률의 비율에서 유도된다. 이를 오즈 함수(odds function)라 하는데 성공확률이 $ p $ 일 때 다음과 같다.
$$ \mathrm{odds}(p) = \frac{p}{1-p} $$
그러나 이 함수의 결과값의 범위는 $[0, \infty] $ 이다. 따라서 이를 직접적으로 확률로서 예측하기 어렵고, 머신러닝에서 활용하려고 하면 오버플로우 위험도 존재한다. 따라서 오즈 함수에 자연로그를 씌운 로짓 함수(logit function)을 활용하는데 다음과 같다.
$$ \mathrm{logit}(p) = \ln [ \mathrm{odds} (p) ] = \ln \left( \frac{p}{1-p} \right) $$
이를 $ z $ 라 하면 다음과 같다.
$$ \ln \left( \frac{p}{1-p} \right) = z $$
알고 싶은 것이 성공확률 $ p $ 이기 때문에 $ p $ 에 대해 정리하면 다음과 같다.
$$ p = \frac{1}{1 + e^{-z}} $$
위에서 나타낸 시그모이드 함수와 같다. 즉 시그모이드 함수는 확률값을 나타낸다.
이진 크로스 엔트로피 (Binary Cross Entropy)
이진 분류 문제에서 손실함수로 많이 사용되는 함수이다. 정의는 아래와 같다.
$$ j ( \mathbf{w}) = - \frac{1}{n} \sum_{i=1}^n \left[ y^{(i)} \ln (\hat{y}^{(i)}) + (1 - y^{(i)}) \ln (1 - \hat{y}^{(i)}) \right] $$
이는 최대가능도법(maximum likelihood method)으로 유도된 함수로 비용함수로서의 역할을 위해 앞에 $ - $ 가 붙었다.
이항 로지스틱 회귀 (Binary Logistic Regression)
로지스틱 회귀는 시그모이드 함수를 이용하여 확률을 예측하고, 이를 통해 분류를 하는 모델이다. 이때 손실함수로 크로스 엔트로피를 사용한다.
이진 분류 모델이라 가정하고 설명하면 회귀모델은 아래와 같다.
$$ \hat{\mathbf{y}} = \frac{1}{1+\exp\left( - \mathbf{X} \mathbf{w} \right)} $$
여기서 $\hat{y} $ 가 임계값(threshold) 이상이면 양성 클래스(positive class)로, 미만이면 음성 클래스(negative class)로 분류한다.
$$ \hat{y}_{\mathrm{class}i} = \begin{cases} 1, & \quad (\hat{y} \geq \mathrm{threshold}) \\ 0, & \quad (\text{otherwise}) \end{cases} $$
경사하강법을 적용하여 학습하기 위해서는 손실함수를 미분해야 하는데, 이진 크로스 엔트로피 함수를 미분하면 다음과 같다.
$$ \triangledown j (\mathbf{w}) = \frac{1}{n} \mathbf{X}^T (\hat{\mathbf{y}} - \mathbf{y}) $$
이를 적용하여 각 가중치를 다음과 같이 업데이트한다.
$$ \mathbf{w} := \mathbf{w} - \alpha \cdot \triangledown j (\mathbf{w}) $$
결국 로지스틱 회귀는 선형 회귀의 출력에 시그모이드 함수를 적용해, 예측값을 확률로 해석하는 형태라고 보면 된다.
두 개의 피처에 대해 로지스틱 회귀를 진행하면 아래와 같은 분류 결과가 나온다.

주요하게 보면 좋은 점은 경계가 선형이라는 것이다. 선형이 아닌 경계를 만들고 싶다면 선형 회귀가 아닌 다른 회귀를 사용하거나 기존값을 변형(transformation)하여 사용해야 한다.
다항 로지스틱 회귀 (Multinomial Logistic Regression)
앞서 이항 로지스틱 회귀는 분류 클래스가 두 종류인 경우에 사용할 수 있었다. 그렇다면 만약 분류해야 하는 클래스가 세 개 이상인 경우는 어떻게 해야할까. 가장 간단하게는 그냥 이진 분류를 여러번 하면 된다. 예를 들어서 클래스를 A, B, C 세개로 분리해야 한다고 해보자. 그렇다면 먼저 클래스 A와 나머지로 분리한다. 그리고 B와 나머지로 분리한다. 그리고 C와 나머지로 분리한다. 그리고 이 경계를 합치면 된다.
그런데 이 경계를 합치는 부분에서는 결국 하나의 확률이 나와야 한다. 따라서 기존 시그모이드 함수를 그대로 사용하는 것이 아니라 소프트맥스(softmax) 함수를 이용해야 한다. 소프트맥스 함수는 다음과 같다.
$$ \mathrm{softmax} = \hat{y}_k = \frac{e^{z_k}}{\sum_i e^{z_i}} $$
여기서 $ k $ 는 각 클래스이다.
소프트맥스 함수 없이 그냥 로짓 함수만을 활용해 계산하면 값들은 숫자일 뿐 확률이 아니다. 그렇다고 앞서 언급한 시그모이드 함수를 이용하면 이진 분류만 되기 때문에 위와 같이 만들어 확률의 합이 $ 1 $ 이 되도록 만들어준다. 이를 고려하여 전체 회귀식을 쓰면 다음과 같다.
$$ \hat{y}_k^{(i)} = \frac{e^{\mathbf{x}^{(i)} \cdot \mathbf{w}_k}}{\sum_{j=1}^{K} e^{\mathbf{x}^{(i)} \cdot \mathbf{w}_j}} $$
클래스는 소프트맥스를 통해 나온 값을 통해 다음과 같이 클래스를 예측한다.
$$ \underset{k}{\arg\max} \text{ } \hat{y}_k $$
다항 로지스틱 회귀의 손실 함수는 각 클래스에 대한 확률과 정답의 크로스 엔트로피를 더한 형태로, 이항 크로스 엔트로피의 일반화된 버전이다.
$$ j ( \mathbf{w}) = - \frac{1}{n} \sum_{i=1}^n \sum_{k=1}^K \left[ y^{(i)}_k \ln (\hat{y}^{(i)}_k) \right] $$
두 개의 피처에 대해 세 개의 클래스를 가지는 다항 로지스틱 회귀 결과는 아래와 시각화할 수 있다.

'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| [ML] K-최근접 이웃(K-NN, K-nearest neighbors) (0) | 2025.04.08 |
|---|---|
| [ML] 결정트리(decision tree)와 랜덤포레스트(random forest) (0) | 2025.04.07 |
| [ML] 정칙화(regularization)와 릿지회귀(ridge regression), 라쏘회귀(LASSO regression), 엘라스틱넷회귀(elastic net regression) (0) | 2025.03.31 |
| [ML] 선형회귀모델(linear regression model) (0) | 2025.03.29 |
| [ML] 분류 모델 평가(evaluation) (0) | 2025.03.29 |