필요 이유
머신러닝에서의 목표는 최적의 가중치(weight)를 구하는 것이다. 최적의 가중치란 손실함수(loss function) 혹은 비용함수(cost function)로 정의된 함수값이 가장 작은 지점에 해당하는 가중치를 의미한다.
수학적으로 최저점을 찾는 가장 간단한 방법은 기울기가 $0$ 되는 지점을 찾고, 그 지점이 최소인지 확인하는 것이다. 간단한 문제, 예를 들어 선형회귀와 같은 문제에서는 이를 통해 최적의 회귀계수를 비교적 쉽게 계산할 수 있다. 이때 기울기가 $0$ 이 되는 지점을 찾기 위한 대표적인 해석적 방법이 정규방정식(normal equation)이다.
$$ X^T X \beta = X^T Y \Rightarrow \hat{\beta} = (X^TX)^{-1} X^T Y $$
이 정규방정식을 이용하면 해를 한 번에 구할 수 있다는 장점이 있지만 독립변수가 많은 다중회귀 문제에서는 계산 비용이 매우 커진다는 단점이 있다. 예를 들어 $ n \times m $ 행렬 $ X $ 가 다중회귀모형에서의 독립변수 행렬이라면, $ X^T X $ 는 $ m \times m $ 행렬이 되며, 이에 대한 역행렬을 계산하는 데는 $ \mathcal{O}(m^3) $ 의 연산량이 필요하다. 변수의 수가 많을수록 계산 비용이 굉장히 커진다는 것을 알 수 있다.
이러한 단점들 때문에 실제 머신러닝에서는 경사 하강법을 이용해 손실함수를 최소화하는 가중치를 점진적으로 찾아나가는 방식을 주로 사용한다. 경사 하강법은 반복적으로 기울기를 따라 이동하면서 손실함수가 최소가 되는 지점에 수렴하도록 한다. 특히 특성 수가 많거나 데이터셋이 큰 경우, 계산 효율성과 확장성 측면에서 매우 유리하다.
경사 하강법 (Gradient Descent)
어떤 손실함수를 다음과 같이 정의하자.
$$ j(\boldsymbol{\theta}) $$
여기서 $ \boldsymbol{\theta} $ 는 가중치 벡터이다. 그리고 목표는 다음과 같다.
$$ \underset{\boldsymbol{\theta}}{\min} j (\boldsymbol{\theta}) $$
즉 $ j (\boldsymbol{\theta}) $ 를 최소화하는 $ \boldsymbol{\theta} $ 를 찾는 것이다. 이를 위해 아래와 같이 미분하여 기울기를 구해보자.
$$ \triangledown j( \boldsymbol{\theta} ) = \left( \frac{\partial j}{\partial \theta_0}, \frac{\partial j}{\partial \theta_1}, \cdots, \frac{\partial j}{\partial \theta_m} \right) $$
이제 생각을 해보자. 기울기가 양수 혹은 음수라는 것은 무엇일까. 구체적으로 $ \theta_0 $ 에 대한 기울기가 양수라면 무엇을 의미할까. 이는 결국 $ \theta_0 $ 가 증가하면 $ j $ 가 증가한다는 뜻이다. 우리는 $ j $ 를 최소화해야 하기 때문에 기울기가 양수라면 $ \theta_0 $ 를 줄여줘야 한다. 반대로 기울기가 음수라면 $ \theta_0 $ 가 증가할 때 $ j $ 가 감소한다는 뜻이고, 따라서 우리는 $ \theta_0 $ 를 증가시켜야 한다.
이를 이용해서 효율적으로 $ \boldsymbol{\theta} $ 를 업데이트 하고 손실함수값을 최소로 하는 지점을 찾는 방법이 경사 하강법이다. 즉 기울기의 반대 방향으로 $ \boldsymbol{\theta}$ 를 업데이트 함으로써 손실함수를 최소로 하는 $ \boldsymbol{\theta} $ 를 찾는 것이다. 이를 위해 다음과 같이 손실함수를 업데이트 한다.
$$ \theta_i = \theta_i - \alpha \frac{\partial j}{\partial \theta_i} $$
여기서 $ \alpha $ 는 학습률(learning rate)로 한번 업데이트에서 얼마나 업데이트할지를 결정한다. 이렇게 경사하강법을 이용해 아래와 같이 최적의 지점을 찾을 수 있다.
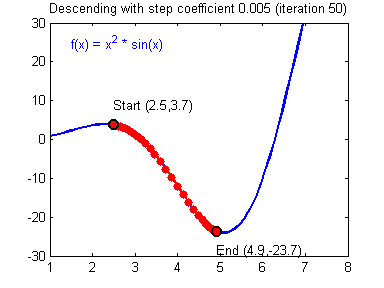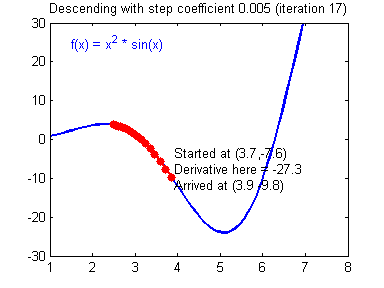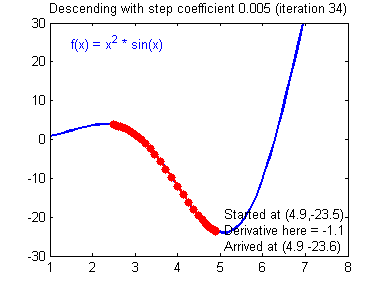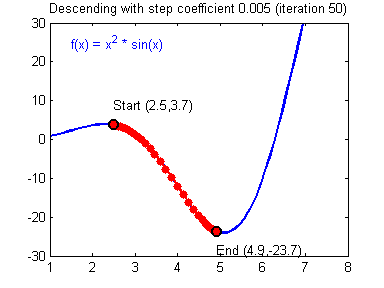
단적으로 피처(feature)가 하나인 경우에 대해서 그려봤지만, 피처가 여러개인 경우에도 마찬가지로 가중치를 업데이트한다.
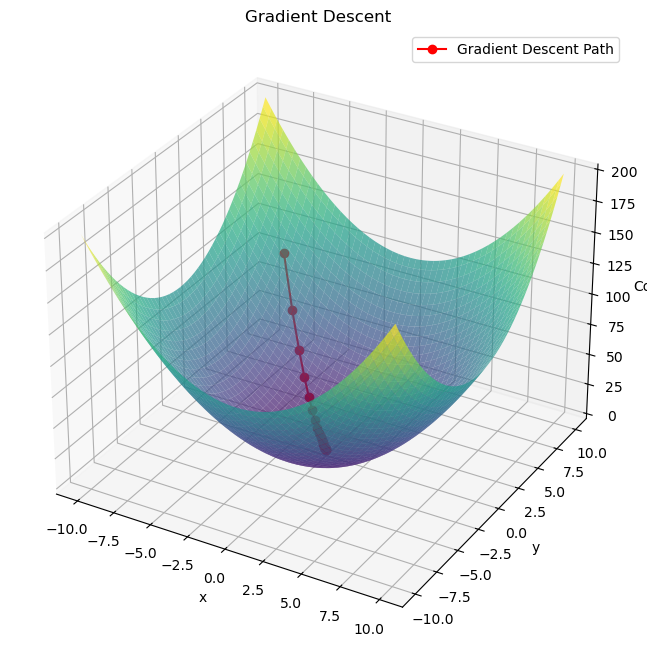
식을 잘보면 기울기에 학습률을 곱한다. 따라서 기울기가 크다면 더 많이 가중치를 조정하고, 기울기가 작으면 더 적게 기울기를 조정한다.
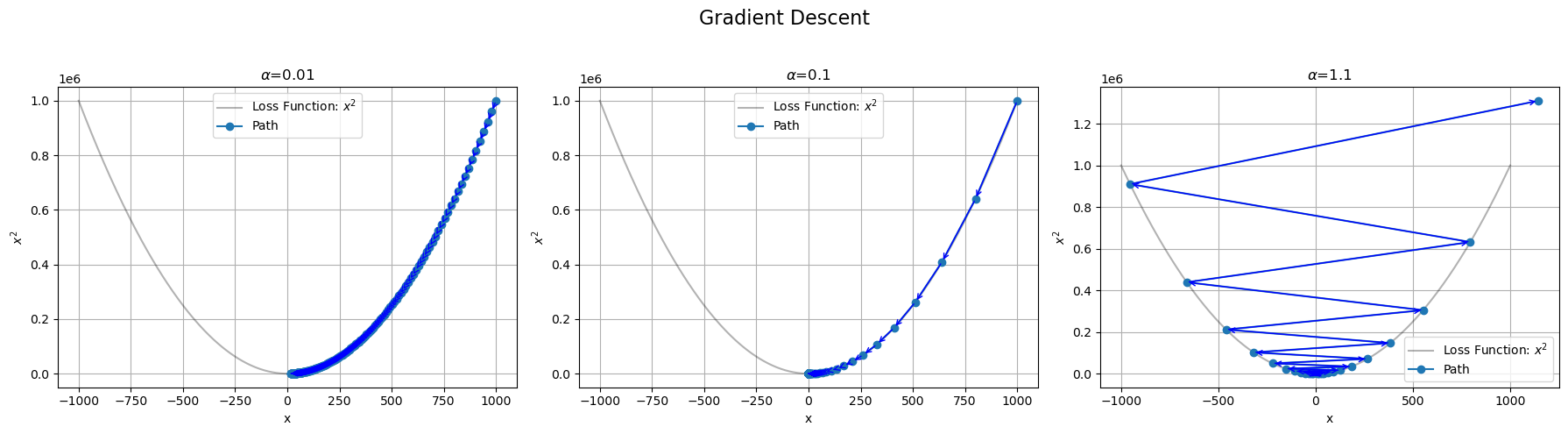
학습률(learning rate) 역시 중요한데, 한 번에 얼마나 가중치를 업데이트 하느냐가 달려있기 때문이다. 학습률이 너무 크다면 손실함수를 최소화하는 지점을 지나쳐서 발산해버릴 여지가 있고, 학습률이 너무 작다면 지역 최소점(local minimum)에 갇혀 학습이 끝날 우려가 있기도 하거니와 학습이 굉장히 느리게 진행되기 때문이다. 아래 그림을 통해 이를 볼 수 있다.
'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| [ML] 정칙화(regularization)와 릿지회귀(ridge regression), 라쏘회귀(LASSO regression), 엘라스틱넷회귀(elastic net regression) (0) | 2025.03.31 |
|---|---|
| [ML] 선형회귀모델(linear regression model) (0) | 2025.03.29 |
| [ML] 분류 모델 평가(evaluation) (0) | 2025.03.29 |
| [ML] 머신러닝 용어 및 개요 (0) | 2025.03.11 |
| [ML] 머신러닝(machine learning) 개념 및 소개 (0) | 2025.02.12 |
필요 이유
머신러닝에서의 목표는 최적의 가중치(weight)를 구하는 것이다. 최적의 가중치란 손실함수(loss function) 혹은 비용함수(cost function)로 정의된 함수값이 가장 작은 지점에 해당하는 가중치를 의미한다.
수학적으로 최저점을 찾는 가장 간단한 방법은 기울기가 $0$ 되는 지점을 찾고, 그 지점이 최소인지 확인하는 것이다. 간단한 문제, 예를 들어 선형회귀와 같은 문제에서는 이를 통해 최적의 회귀계수를 비교적 쉽게 계산할 수 있다. 이때 기울기가 $0$ 이 되는 지점을 찾기 위한 대표적인 해석적 방법이 정규방정식(normal equation)이다.
$$ X^T X \beta = X^T Y \Rightarrow \hat{\beta} = (X^TX)^{-1} X^T Y $$
이 정규방정식을 이용하면 해를 한 번에 구할 수 있다는 장점이 있지만 독립변수가 많은 다중회귀 문제에서는 계산 비용이 매우 커진다는 단점이 있다. 예를 들어 $ n \times m $ 행렬 $ X $ 가 다중회귀모형에서의 독립변수 행렬이라면, $ X^T X $ 는 $ m \times m $ 행렬이 되며, 이에 대한 역행렬을 계산하는 데는 $ \mathcal{O}(m^3) $ 의 연산량이 필요하다. 변수의 수가 많을수록 계산 비용이 굉장히 커진다는 것을 알 수 있다.
이러한 단점들 때문에 실제 머신러닝에서는 경사 하강법을 이용해 손실함수를 최소화하는 가중치를 점진적으로 찾아나가는 방식을 주로 사용한다. 경사 하강법은 반복적으로 기울기를 따라 이동하면서 손실함수가 최소가 되는 지점에 수렴하도록 한다. 특히 특성 수가 많거나 데이터셋이 큰 경우, 계산 효율성과 확장성 측면에서 매우 유리하다.
경사 하강법 (Gradient Descent)
어떤 손실함수를 다음과 같이 정의하자.
$$ j(\boldsymbol{\theta}) $$
여기서 $ \boldsymbol{\theta} $ 는 가중치 벡터이다. 그리고 목표는 다음과 같다.
$$ \underset{\boldsymbol{\theta}}{\min} j (\boldsymbol{\theta}) $$
즉 $ j (\boldsymbol{\theta}) $ 를 최소화하는 $ \boldsymbol{\theta} $ 를 찾는 것이다. 이를 위해 아래와 같이 미분하여 기울기를 구해보자.
$$ \triangledown j( \boldsymbol{\theta} ) = \left( \frac{\partial j}{\partial \theta_0}, \frac{\partial j}{\partial \theta_1}, \cdots, \frac{\partial j}{\partial \theta_m} \right) $$
이제 생각을 해보자. 기울기가 양수 혹은 음수라는 것은 무엇일까. 구체적으로 $ \theta_0 $ 에 대한 기울기가 양수라면 무엇을 의미할까. 이는 결국 $ \theta_0 $ 가 증가하면 $ j $ 가 증가한다는 뜻이다. 우리는 $ j $ 를 최소화해야 하기 때문에 기울기가 양수라면 $ \theta_0 $ 를 줄여줘야 한다. 반대로 기울기가 음수라면 $ \theta_0 $ 가 증가할 때 $ j $ 가 감소한다는 뜻이고, 따라서 우리는 $ \theta_0 $ 를 증가시켜야 한다.
이를 이용해서 효율적으로 $ \boldsymbol{\theta} $ 를 업데이트 하고 손실함수값을 최소로 하는 지점을 찾는 방법이 경사 하강법이다. 즉 기울기의 반대 방향으로 $ \boldsymbol{\theta}$ 를 업데이트 함으로써 손실함수를 최소로 하는 $ \boldsymbol{\theta} $ 를 찾는 것이다. 이를 위해 다음과 같이 손실함수를 업데이트 한다.
$$ \theta_i = \theta_i - \alpha \frac{\partial j}{\partial \theta_i} $$
여기서 $ \alpha $ 는 학습률(learning rate)로 한번 업데이트에서 얼마나 업데이트할지를 결정한다. 이렇게 경사하강법을 이용해 아래와 같이 최적의 지점을 찾을 수 있다.

단적으로 피처(feature)가 하나인 경우에 대해서 그려봤지만, 피처가 여러개인 경우에도 마찬가지로 가중치를 업데이트한다.

식을 잘보면 기울기에 학습률을 곱한다. 따라서 기울기가 크다면 더 많이 가중치를 조정하고, 기울기가 작으면 더 적게 기울기를 조정한다.
학습률(learning rate) 역시 중요한데, 한 번에 얼마나 가중치를 업데이트 하느냐가 달려있기 때문이다. 학습률이 너무 크다면 손실함수를 최소화하는 지점을 지나쳐서 발산해버릴 여지가 있고, 학습률이 너무 작다면 지역 최소점(local minimum)에 갇혀 학습이 끝날 우려가 있기도 하거니와 학습이 굉장히 느리게 진행되기 때문이다. 아래 그림을 통해 이를 볼 수 있다.

'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| [ML] 정칙화(regularization)와 릿지회귀(ridge regression), 라쏘회귀(LASSO regression), 엘라스틱넷회귀(elastic net regression) (0) | 2025.03.31 |
|---|---|
| [ML] 선형회귀모델(linear regression model) (0) | 2025.03.29 |
| [ML] 분류 모델 평가(evaluation) (0) | 2025.03.29 |
| [ML] 머신러닝 용어 및 개요 (0) | 2025.03.11 |
| [ML] 머신러닝(machine learning) 개념 및 소개 (0) | 2025.02.12 |