이항 관계 (Binary Relation)
어떤 집합에서 다른 집합으로의 관계(relation)는 첫 번째 집합의 요소들이 두 번째 집합의 어떤 요소들과 관련되어 있는지로 확인할 수 있다. 예를 들어 자연수의 영역에서 정의된 항등함수를 생각하면, $ \{(1, 1), (2, 2), \cdots, (n, n) \} $ 으로 나타낼 수 있을 것이다.
즉 집합 $ X $ 에서 집합 $ Y $ 로의 관계(여기서는 두 집합의 관계이므로 이항관계) $ R $ 은 $ X \times Y $ 의 부분집합이다. 만약 $ (x, y) \in R $ 이면, $ x \text{ } R \text{ } y $ 라 쓰고 $ x $ 가 $ y $ 와 관계있다고 말한다. 이 후 관계라 하면 이항 관계를 말한다.
이때 관계 $ R $ 의 원소인 순서쌍에서 첫번째 원소의 집합을 정의역(domain)이라 하고, 두번째 원소의 집합을 치역(range)이라 하고, 두번째 원소가 포함되어 있는 집합을 공역(codomain)이라 한다. 함수에서의 정의와 같다.
방향 그래프 (Directed Graph)
관계는 방향 그래프(directed graph)를 통해 나타낼 수 있다. 집합 $ X $ 에서의 관계를 방향 그래프로 나타낸다하면, 먼저 집합 $ X $ 의 요소들을 나타내는 정점을 그린다. 그 후 $ (x, y) $ 를 그리는데, $ x $ 에서 $ y $ 로 가는 화살표인 방향 간선(directed edge)을 그린다. 만약 $ x $ 에서 $ x $ 로 가는 방향 간선이 있다면 루프(loop)라 한다.
예를 들어 $ X = \{ 1, 2, 3, 4 \} $ 에 대해 $ x \leq y $ 이고 $ x, y \in X $ 일 때 정의된 관계 $ R $ 을 방향 그래프로 본다면 아래와 같다.
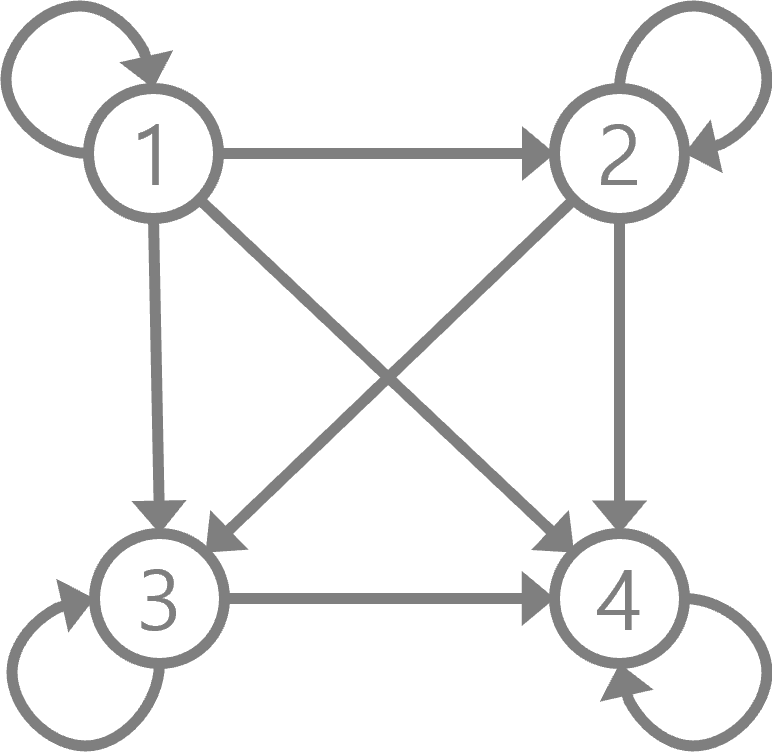
관계 행렬 (Matrices of Relations)
관계를 행렬로 표현할 수 있다. 임의의 순서대로 정의역 $ X $ 의 요소들을 행에, 치역 $ Y $ 의 요소들을 열에 레이블링 한다. 만약 $ x \text{ } R \text{ } y $ 이면, 행 $ x $ 와 열 $ y $ 의 값을 $ 1 $ 로 설정하고, 만약 아니라면 $ 0 $ 으로 설정한다.
만약 집합 $ X $ 에서의 관계 $ R $ 의 행렬을 작성한다면, 즉 정의역과 치역이 동일하다면 행과 열 모두 동일한 순서를 사용한다. 또한 이 행렬은 정사각행렬이다.
예를 들어 관계 $ R = \{ (a, a), (b, b), (c, c), (d, d), (b, c), (c, b)\} $ 를 관계 행렬로 나타내면 아래와 같다.
$$ \begin{array}{c|cccc} & a & b & c & d \\ \hline a & 1 & 0 & 0 & 0 \\ b & 0 & 1 & 1 & 0 \\ c & 0 & 1 & 1 & 0 \\ d & 0 & 0 & 0 & 1 \\ \end{array} $$
관계의 성질
$ R $ 을 집합 $ X $ 에서의 관계라 할 때 다음이 성립한다.
- 반사적 (Reflexive)
$ \forall x \in X $, $ (x, x) \in R $
$ R $ 이 위를 만족하면 반사적이라 한다. 모든 정점에 루프가 있는 것이다.
- 비반사적 (Irreflexive)
$ \forall x \in X $, $ (x, x) \notin R $
$ R $ 이 위를 만족하면 비반사적이라 한다. 모든 정점에 루프가 없는 것이다.
- 대칭적 (Symmetric)
$ \forall x, y \in X $, $ (x, y) \in R \to (y, x) \in R $
$ R $ 이 위를 만족하면 대칭적이라 한다. 즉 방향 그래프로 그렸을 때 $ v $ 에서 $ w $ 로 가는 방향 간선이 있으면 $ w $ 에서 $ v $ 로 가는 방향 간선도 있다.
- 반대칭적 (Antisymmetric)
$ \forall x, y \in X $, $ (x, y) \in R \land (y, x) \in R \to x = y $
$ R $ 이 위를 만족하면 반대칭적이라 한다. 참고로 대우는 $ \forall x, y \in X $, $ x \neq y \to (x, y) \notin R \lor (y, x) \notin R $ 이다. 방향 그래프로 그렸을 때 서로 다른 두 정점 사이에는 최대 하나의 방향 간선만 존재하는 경우이다. $ w \neq v $ 일 때 $ w $ 에서 $ v $ 로 가는 방향 간선이 있다면 $ v $ 에서 $ w $ 로 가는 방향 간선은 존재할 수 없다.
주의해야 할 것은 반대칭적(antisymmetric)이라는 것과 대칭적이지 않다는 것(not symmetric)은 다르다는 것이다. 예를 들어 집합 $ X = \{ a, b\} $ 에서의 관계 $ R = \{(a, a), (b, b) \} $ 는 대칭적이며, 반대칭적이고, 반사적이다.
- 비대칭적 (Asymmetric)
$ \forall x, y \in X $, $ (x, y) \in R \to (y, x) \notin R $
$ R $ 이 위를 만족하면 비대칭적이라 한다. 즉 방향 그래프를 그렸을 때, 반대칭적이면서 루프도 없어야 한다.
- 추이적 (Transitive)
$ \forall x, y, z \in X $, $ (x, y) \in R \land (y, z) \in R \to (x, z) \in R $
$ R $ 이 위를 만족하면 추이적이라 한다. 즉 $ x $ 에서 $ y $ 로 가는 방향 간선과 $ y $ 에서 $ z $ 로 가는 방향 간선이 있다면, $ x $ 에서 $ z $ 로 가는 방향 간선도 존재해야 한다.
- 반순서 (Partial Order)
관계는 집합의 요소들을 정렬하는 데에 사용될 수 있다. 예를 들어 정수 집합에 대해 $ (x, y) \in R $ 일 때, $ x \leq y $ 로 정의된 관계 $ R $ 은 정수들을 정렬한다. 이 관계 $ R $ 은 반사적이고, 반대칭적이며, 추이적임을 알 수 있다.
만약 집합 $ X $ 에서의 관계 $ R $ 이 반사적이고, 반대칭적이며, 추이적이면 $ R $ 을 반순서라 한다.
$ R $ 이 집합 $ X $ 에서의 반순서일 경우, $ x \leq y $ 는 $ x \text{ } R \text{ } y $, 즉 $ (x, y) \in R $ 을 나타내는 표기법으로 사용되기도 한다.
$ R $ 이 집합 $ X $ 에서의 반순서일 경우, 만약 $ x, y \in X $ 이고, $ x \leq y $ 거나, $ y \leq x $ 라면 $ x $ 와 $ y $ 가 비교 가능(comparable)하다고 말한다. 만약 $ X $ 의 모든 요소 쌍이 비교 가능하다면, $ R $ 을 전순서(total order)라 한다.
역관계 (Inverse Relation)
$$ R^{-1} = \{ (y, x) \mid (x, y) \in R \} $$
관계 $ R $ 이 있을 때 역관계 $ R^{-1} $ 는 위를 만족한다.
방향 그래프로 본다면 방향 간선의 방향을 반대로 그리면 역관계이다.
합성관계 (Composite Relation)
관계 $ R_1 $ 이 집합 $ X $ 에서 집합 $ Y $ 로의 관계이고, 관계 $ R_2 $ 가 집합 $ Y $ 에서 집합 $ Z $ 로의 관계일 때, $ R_1 $ 과 $ R_2 $ 의 합성은 $ R_2 \circ R_1 $ 으로 표기되며, $ X $ 에서 $ Z $ 로의 관계로 정의된다.
$$ R_2 \circ R_1 = \{ (x, z) \mid x \in X, z \in Z, (x, y) \in R_1, (y, z) \in R_2 \} $$
결국 $ R_1 $ 의 공역이 $ R_2 $ 의 정의역인 경우에만 합성관계를 만들 수 있다.
동치관계 (Equivalence Relation)
$ X $ 의 원소들로 이루어진 비어 있지 않은 부분집합들의 모임 $ \mathcal{P} $ 가 분할(partition)이라 불리기 위해서는 $ X $ 의 모든 원소가 $ \mathcal{P} $ 의 정확히 하나의 원소에 속해야 한다. 즉 아래를 만족해야 한다.
$ S_i, S_j \in \mathcal{P} \land i \neq j \to S_i \cap S_j = \emptyset $ $ \left( X = \bigcup_{S \in \mathcal{P}} S, \text{ } \emptyset \notin \mathcal{P} \right) $
$ \mathcal{P} $ 가 집합 $ X $ 의 분할일 때, $ x \text{ } R \text{ } y $ 는 $ \mathcal{P} $ 의 어떤 집합 $ S $ 에서 $ x \in S $ 이고 $ y \in S $ 인 것을 의미한다고 정의하자. 즉 다음과 같다.
$$ R = \{ (x, y) \mid S \in \mathcal{P}, x \in S, y \in S \} $$
그렇다면 $ R $ 은 반사적, 대칭적, 추이적이다.
$ x \in X $ 라 할 때, 분할의 정의에 따라, $ x $ 는 $ \mathcal{P} $ 의 어떤 원소 $ S $ 에 속하고, 따라서 $ x \text{ } R \text{ } x $, 즉 $ R $ 은 반사적이다.
$ x \text{ } R \text{ } y $ 라 할 때, $ x $ 와 $ y $ 는 $ \mathcal{P} $ 의 어떤 집합 $ S $ 에 속하고, $ y $ 와 $ x $ 또한 $ S $ 에 속하므로 $ y \text{ } R \text{ } x $ 가 성립하며, 따라서 $ R $ 은 대칭적이다.
$ x \text{ } R \text{ } y $ 이고 $ y \text{ } R \text{ } z $ 라 할 때, $ x $ 와 $ y $ 는 $ \mathcal{P} $ 의 어떤 집합 $ S $ 에 속하고, $ y $ 와 $ z $ 는 다른 집합 $ T $ 에 속한다. 그러나 $ y $ 는 $ \mathcal{P} $ 의 정확히 하나의 원소에 속하므로 $ S = T $ 가 성립한다. 따라서 $ x $ 와 $ z $ 는 $ S $ 에 속하고, $ x \text{ } R \text{ } z $ 가 성립하며 추이적이다.
$ \mathcal{P} $ 와 $ R $ 이 위와 같이 주어지고, $ S \in \mathcal{P} $ 라면 $ S $ 의 원소들은 관계 $ R $ 의 의미에서 동치로 간주될 수 있다. 이는 반사적, 대칭적, 추이적 관계를 동치관계라 부르는 이유가 된다. 즉 어떤 집합 $ X $ 에서 반사적, 대칭적, 추이적인 관계를 동치관계라 한다. 어떤 분할 $ \mathcal{P} $ 에도 그에 대응하는 동치관계 $ R $ 이 존재한다.
동치류 (Equivalence Classes)
집합 $ X $ 에 대한 동치관계가 주어졌을 때, $ X $ 에 관계된 원소들을 그룹화하여 $ X $ 를 분할할 수 있고, 서로 관계인 원소들은 동등하다(equivalent)고 생각할 수 있다.
$ R $ 이 집합 $ X $ 에서의 동치관계라 할 때, $ a \in X $ 에 대해 $ [a] = \{x \in X \mid x \text{ } R \text{ } a \} $ 라 정의하자. 그렇다면 $ \mathcal{P} = \{ [a] \mid a \in X \} $ 는 $ X $ 의 분할이 된다.
$ \mathcal{P} $ 가 $ X $ 의 분할이 된다는 것은 $ X $ 의 모든 원소가 $ \mathcal{P} $ 의 정확히 하나의 원소에 속한다는 것과 같다.
$ a \in X $ 라 하자. $ a \text{ } R \text{ } a $ 이므로 $ a \in [a] $ 이고, 따라서 $ X $ 의 모든 원소는 적어도 하나의 $ \mathcal{P} $ 의 원소에 속한다.
모든 $ c, d \in X $ 에 대해 만약 $ c \text{ } R \text{ } d $ 라면 $ [c] = [d] $ 인데 증명은 다음과 같다. $ c \text{ } R \text{ } d $ 라 가정하면 $ x \in [c] $ 일 때 $ x \text{ } R \text{ } c $ 이다. $ c \text{ } R \text{ } d $ 이고 $ R $ 은 추이적이므로 $ x \text{ } R \text{ } d $ 이다. 따라서 $ x \in [d] $ 이므로 $ [c] \subseteq [d] $ 이다. 비슷하게 $ [d] \subseteq [c] $ 이므로 $ [c] = [d] $ 이다.
$ x \in X $ 이고, $ x \in [a] $ 이면서 $ x \in [b] $ 라 가정하면 $ x \text{ } R \text{ } a $ 이고 $ x \text{ } R \text{ } b $ 이다. 그렇다면 $ [x] = [a] $ 이고, $ [x] = [b] $ 이므로 $ [a] = [b] $ 이다. 따라서 $ X $ 의 모든 원소는 $ \mathcal{P} $ 의 정확히 하나의 원소에 속한다.
이때 $ [a] $ 는 $ X $ 에서 $ a $ 와 관련된 모든 원소들의 집합이고, 집합 $ [a] $ 를 $ R $ 에 의해 주어진 $ X $ 의 동치류라 한다.
$ R $ 이 유한 집합 $ X $ 의 동치관계라 하고, 각 동치류가 $ r $ 개의 원소를 가지고 있다면, 동치류의 개수는 $ \dfrac{|X|}{r} $ 이다.
$ X_1, X_2, \dots , X_k $ 가 서로 다른 동치류라 하자. 이 집합들이 $ X $ 를 분할하므로, $ |X| = |X_1| + |X_2| + \cdots + |X_k| = r + r + \cdots + r = kr $ 이다.
따라서 $ k = \dfrac{|X|}{r} $ 이다.
'Mathematics > Discrete Mathematics' 카테고리의 다른 글
| [Discrete Mathematics] 약수(divisor)와 소수(prime) 그리고 최대공약수와 최소공배수 (0) | 2024.10.15 |
|---|---|
| [Discrete Mathematics] 알고리즘(algorithms) 및 알고리즘 분석 (0) | 2024.10.12 |
| [Discrete Mathematics] 수열(sequence)과 문자열(string) (0) | 2024.10.08 |
| [Discrete Mathematics] 함수(function)의 정의와 성질을 통한 분류 (0) | 2024.10.08 |
| [Discrete Mathematics] 바닥 함수와 천장 함수 (0) | 2024.10.07 |