퀵 정렬

정렬을 사용할 때 일반적인 상황에서 가장 우수한 정렬 방법 중 하나이다. 분할정복법을 활용하는데, 리스트를 두개의 부분리스트로 비균등 분할하고 임시 정렬한 후 다시 분할하는 방법으로 정렬한다.
피벗, 즉 축을 정해서 축을 기준으로 피벗보다 작은 값과 피벗보다 큰 값으로 분할하고 다시 그렇게 분할된 리스트에서 피벗을 설정하고 그 피벗을 기준으로 작은 값과 큰 값으로 분할하고, 다시 그렇게 분할된 리스트에서... 반복하여 정렬하는 방식이다. 왼쪽부터 오른쪽으로의 탐색이 하나, 오른쪽에서 왼쪽으로의 탐색이 하나 있어 만약 왼쪽에서 오른쪽으로 이동하다가 피벗보다 큰 값을 만나면 멈추고, 오른쪽에서 왼쪽으로 이동하다가 피벗보다 작은 값을 만나면 멈춘다. 두개 모두 멈추면 두 값을 교환하고, 다시 반복한다. 만약 왼쪽에서의 탐색와 오른쪽에서의 탐색이 만나면 만난 곳의 왼쪽 값, 즉 피벗보다 작은 값과 피벗을 교환한다. 그 후 피벗을 중심으로 왼쪽과 오른쪽으로 분할하고 이를 반복하여 정렬한다.
어떤 값을 피벗값으로 사용하느냐가 중요하다. 피벗값이 잘 선택되어 피벗이 정렬이 끝났을 때 중앙과 교환되어 분할이 균등하게 분할되면, 혹은 균등 분할과 가까운 분할이 이뤄지면 효율이 좋지만, 비균등 분할, 그 중에서도 최악인 것은 피벗값이 해당 리스트에서 가장 작거나 가장 큰 경우 효율이 굉장히 안 좋아진다. 특히 가장 주의해야 하는 것이 이 최악의 경우가 바로 정렬이 완료된 경우라는 것이다. 정렬이 완료된 경우에 일반적으로 선택하는 가장 왼쪽 혹은 오른쪽 값을 선택하면 당연히 가장 작은 값 혹은 가장 큰 값이 선택되기 때문에 피벗값 외의 값이 모두 피벗값보다 크거나 작아 분할이 피벗값 대 나머지 모두로 이뤄지게 되어 효율이 안 좋아진다. 물론 이를 방지하기 위해 피벗값 선택을 다양한 방식으로 시도하지만, 결국 특정하게 정렬된 리스트에서 어쩔 수 없이 효율이 떨어진다.
분할 방법 때문에 안정적이지 못한 정렬 방법이다. 이 때문에 몇몇 언어에서는 기본 라이브러리로 지원하는데 몇몇 언어에서는 기본 라이브러리로 지원하지 않는다.
예시

예를 들어 위와 같은 리스트를 정렬한다고 해보자.

가장 앞 값을 피벗값으로 선택하고 탐색을 시작한다.


$$ \vdots $$


탐색된 값이 없으므로 피벗값과 끝 값을 교환한다.
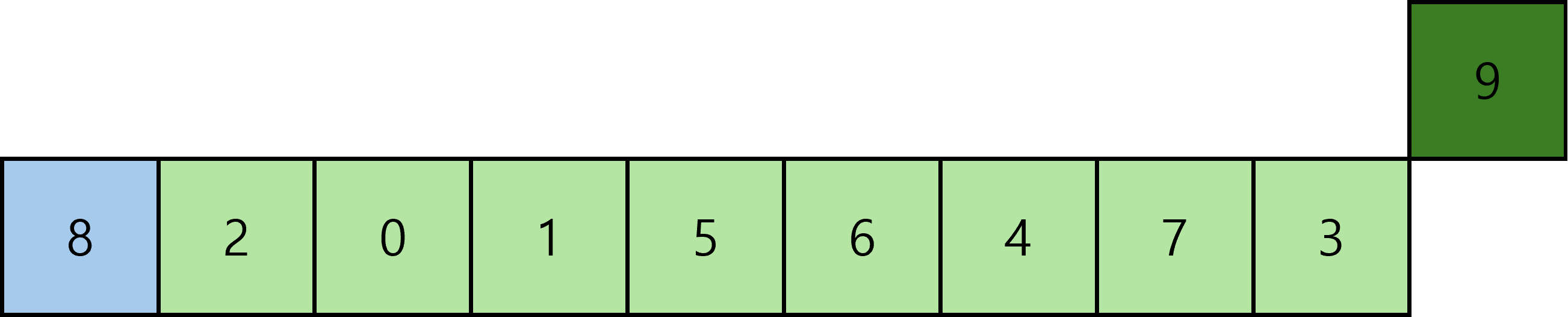
피벗값이 교환된 위치를 기준으로 분할한다. 오른쪽 9는 분할되면서 크기가 1이라 정렬이 완료된 상태이다. 다시 탐색을 시작하면 아래와 같이 탐색이 끝나고 이번에도 탐색된 값이 없으므로 교환하고 분할한다.



$$ \vdots $$

피벗값보다 큰 값이 발견되었다. 이제 오른쪽에서 탐색을 시작한다.

$$ \vdots $$

오른쪽에서도 탐색에 성공하였다. 그런데 오른쪽에서 시작한 인덱스가 왼쪽에서 시작한 인덱스보다 작아졌으므로 피벗값과 교환한다.
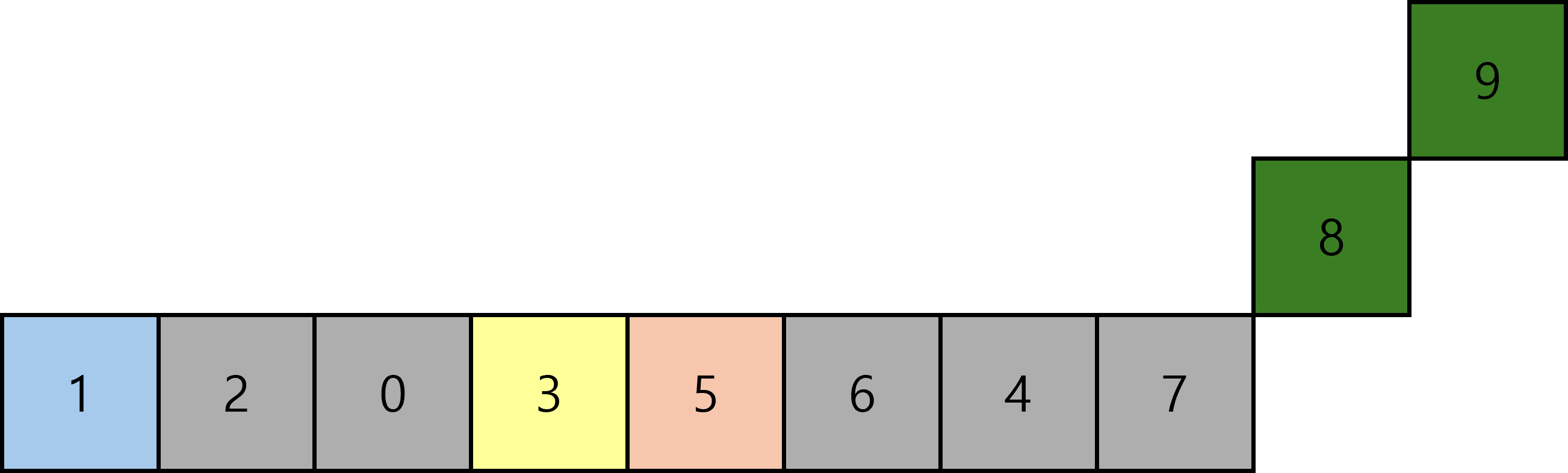
다시 피벗값을 기준으로 분할한다.


피벗을 설정하고 탐색을 시작한다.

큰 값을 찾았다.

작은 값을 찾았다. 오른쪽에서 시작한 인덱스가 왼쪽에서 시작한 인덱스보다 크므로 두 값을 교환한다.

교환 후 다시 이동한다.

작은 값을 다시 찾았고 교환한다.

분할될 공간이 3보다 작으므로 정렬이 완료되었다.

나머지도 정렬해준다.

$$ \vdots $$

이렇게 정렬이 완료된다. 가장 처음 9와 8에서 보이듯이 극단적으로 쏠린 분할이 이뤄지면 효율이 떨어진다.
일반적으로 분할만 잘 이루어지면 $ \mathcal{O} (n \log_2 n) $ 으로 준수한 성능을 보이지만, 분할이 예시에서 9와 8처럼 극단적으로만 이루어지는 경우 $ \mathcal{O} (n^2) $ 의 시간복잡도를 가진다.
구현 | C
void quick_sort(int list[], int left, int right) {
if (left < right) {
int low = left;
int high = right + 1;
int pivot = list[left];
do {
do {
low++;
} while (low <= right && list[low] < pivot);
do {
high--;
} while (high >= left && list[high] > pivot);
if (low < high) {
int temp = list[low];
list[low] = list[high];
list[high] = temp;
}
} while (low < high);
int temp = list[left];
list[left] = list[high];
list[high] = temp;
quick_sort(list, left, high-1);
quick_sort(list, high+1, right);
}
}
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] 병합 정렬(merge sort) (0) | 2024.11.27 |
|---|---|
| [Data Structure] 힙 정렬(heap sort) (0) | 2024.11.26 |
| [Data Structure] 셸 정렬(Shell's sort) (0) | 2024.11.26 |
| [Data Structure] 삽입 정렬(insertion sort) (0) | 2024.11.26 |
| [Data Structure] 선택 정렬(selection sort) (0) | 2024.11.23 |