https://www.acmicpc.net/problem/1004
문제
출발점에서 도착점까지 이동하면서 최소한의 행성계만 진입/이탈하려 한다.
이때 행성계를 진입/이탈하는 횟수를 구하는 문제이다.
단 행성계의 경계가 서로 맞닿거나 교차하는 경우는 없고, 출발점과 도착점이 행성계 경계에 걸친 경우도 없다.
풀이
행성계의 경계가 서로 맞닿거나 교차하는 경우가 있었다면 복잡해졌겠지만 다행히 이 경우는 없다. 따라서 행성계의 진입/이탈 횟수를 구하는 것은 출발점과 도착점이 얼마나 많은 행성계 안에 있는지 구하면 쉽게 확인할 수 있다. 예를 들어서 문제에 예시 그림을 보면 출발점은 한 개의 행성계 안에 있고, 도착점은 두 개의 행성계 안에 있으므로 총 세 번의 진입/이탈이 일어난다.
만약 행성계의 경계가 서로 맞닿거나 교차하는 경우가 있었더라면 이 방법은 쓸 수 없다. 예를 들어 문제 예시 그림이 아래와 같았다면 행성계 진입/이탈 횟수는 세 번 이상으로 늘어난다.
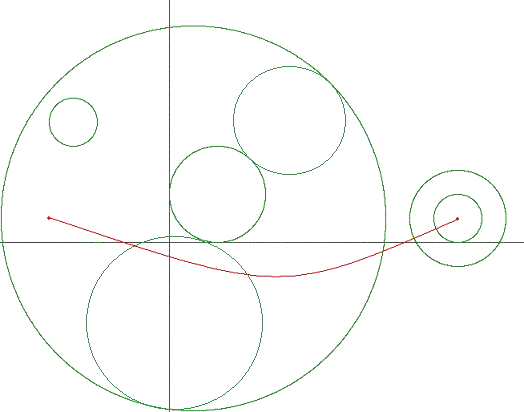
그러나 이 문제에서 조건을 주었기 때문에 위 방법을 쓸 수 있는 것이다.
다시 돌아와서 행성계의 내부에 있는지 확인하는 방법은 두 점 사이 거리 공식을 이용하면 된다. 행성계의 중심점과 행성계의 반지름이 주어지기 때문에 만약 출발점 혹은 도착점과 행성계의 중심점 간의 거리가 반지름보다 작다면 출발점 혹은 도착점이 해당 행성계 내부에 있는 것이다.
단 출발점과 도착점이 같은 행성계 내부에 있다면 출발점에서 도착점으로 이동하면서 진입/이탈은 필요하지 않기 때문에 이 경우는 진입/이탈 횟수를 세지 말아야 한다.
참고로 두 점 $ (x_1, y_1) $ , $ (x_2, y_2) $ 이 있을 때 두 점 사이 거리 공식은 아래와 같다.
$$ \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
루트가 있으면 부정확한 float 형 연산이 있을 수 있기 때문에 아래 코드에서는 행성계 반지름을 제곱하여 출발점과 도착점 간 거리와 비교하였다.
코드
test = int(input())
for _ in range(test):
ans = 0
start_x, start_y, end_x, end_y = map(int, input().split())
planet_n = int(input())
for _ in range(planet_n):
planet_x, planet_y, planet_radius = map(int, input().split())
start_dis = (planet_x - start_x) ** 2 + (planet_y - start_y) ** 2
end_dis = (planet_x - end_x) ** 2 + (planet_y - end_y) ** 2
planet_radius = planet_radius ** 2
if start_dis < planet_radius and end_dis < planet_radius:
continue
elif start_dis < planet_radius:
ans += 1
elif end_dis < planet_radius:
ans += 1
print(ans)
'Online Judge > Baekjoon' 카테고리의 다른 글
| [Baekjoon 9493] 길면 기차, 기차는 빨라, 빠른 것은 비행기 | Python (0) | 2024.08.30 |
|---|---|
| [Baekjoon 5698] Tautogram | Python (0) | 2024.08.30 |
| [Baekjoon 5692] 팩토리얼 진법 | Python (0) | 2024.08.29 |
| [Baekjoon 28432] 끝말잇기 | Python (0) | 2024.08.29 |
| [Baekjoon 27065] 2022년이 아름다웠던 이유 | Python (0) | 2024.08.27 |
